题目内容
已知f(x)=
sin(π+ωx)sin(
-ωx)-cos2ωx(ω>0)的最小正周期为T=π.
(1)求f(
)的值;
(2)在△ABC中,角A、B、C所对应的边分别为a、b、c,若有(2a-c)cosB=bcosC,则求角B的大小以及
f(A)的取值范围.
| 3 |
| 3π |
| 2 |
(1)求f(
| 2π |
| 3 |
(2)在△ABC中,角A、B、C所对应的边分别为a、b、c,若有(2a-c)cosB=bcosC,则求角B的大小以及
f(A)的取值范围.
考点:三角函数中的恒等变换应用,正弦定理
专题:三角函数的求值
分析:(1)先逆用两角差的正弦公式化成正弦型函数的标准形式,然后利用周期公式T=π,求ω的值,进而写出函数f(x)的解析式;求出f(
)的值.
(2)利用正弦定理,求出cosB的值,继而求出B的大小,再根据A为三角形的内角求出A的范围,继而求出f(A)的范围.
| 2π |
| 3 |
(2)利用正弦定理,求出cosB的值,继而求出B的大小,再根据A为三角形的内角求出A的范围,继而求出f(A)的范围.
解答:
解:(1)∵f(x)=
sin(π+ωx)sin(
-ωx)-cos2ωx,
=
sinωxcosωx-cos2ωx,
=
sin2ωx-
cos2ωx-
,
=sin(2ωx-
)-
∴函数f(x)的最小正周期为T=π.
即:
=π,得ω=1,
∴f(x)=sin(2x-
)-
,
∴f(
)=sin(2×
-
)-
=sin
-
=-1,
(2)∵(2a-c)cosB=bcosC,
∴由正弦定理可得:(2sinA-sinC)cosB=sinBsinC,
∴2sinAcosB=sinBcosC+cosBsinC=sin(B+C)=sinA,
∵sinA>0,
∴cosB=
,
∵B∈(0,π),
∴B=
,
∵A+C=π-B=
π,
∴A∈(0,
π),
∴2A-
∈(-
,
),
∴sin(2A-
)∈(-
,1],
∴f(A)=sin(2A-
)-
∈(-1,
],
| 3 |
| 3π |
| 2 |
=
| 3 |
=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=sin(2ωx-
| π |
| 6 |
| 1 |
| 2 |
∴函数f(x)的最小正周期为T=π.
即:
| 2π |
| 2ω |
∴f(x)=sin(2x-
| π |
| 6 |
| 1 |
| 2 |
∴f(
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| 1 |
| 2 |
| 7π |
| 6 |
| 1 |
| 2 |
(2)∵(2a-c)cosB=bcosC,
∴由正弦定理可得:(2sinA-sinC)cosB=sinBsinC,
∴2sinAcosB=sinBcosC+cosBsinC=sin(B+C)=sinA,
∵sinA>0,
∴cosB=
| 1 |
| 2 |
∵B∈(0,π),
∴B=
| π |
| 3 |
∵A+C=π-B=
| 2 |
| 3 |
∴A∈(0,
| 2 |
| 3 |
∴2A-
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴sin(2A-
| π |
| 6 |
| 1 |
| 2 |
∴f(A)=sin(2A-
| π |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角变换及解三角形,第(1)问解决的关键是化成正弦型函数的标准形式;第(2)的关键是把求角的范围转化成先求角的余弦值的范围.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
当x≠0时,有不等式( )
| A、ex<1+x |
| B、当x>0时,ex<1+x;当x<0时,ex>1+x |
| C、ex>1+x |
| D、当x<0时,ex<1+x;当x>0时,ex<1+x |
等比数列{an}各项为正数,且a2a4+a4a6+2a3a5=9,则a3+a5的值为( )
| A、3 | B、6 | C、9 | D、12 |
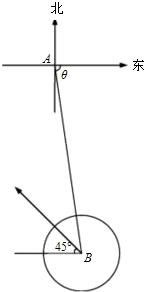 据气象台预报,一台风中心位于某沿海城市A东偏南θ(cosθ=
据气象台预报,一台风中心位于某沿海城市A东偏南θ(cosθ=