题目内容
一个口袋内有4个不同的红球,6个不同的白球.
(1)从中任取4个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取4个球,使总分不大于6分的取法有多少种?.
(1)从中任取4个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取4个球,使总分不大于6分的取法有多少种?.
考点:计数原理的应用
专题:排列组合
分析:(1)由题意可以分三类,红球4个,红球3个和白球1个,红球2个和白球2个,根据计数原理即可得到答案.
(2)从中任取4个球,使总分不大于6分情况有,4白,3白1红,2白2红,根据计数原理即可得到答案.
(2)从中任取4个球,使总分不大于6分情况有,4白,3白1红,2白2红,根据计数原理即可得到答案.
解答:
解:(1)从中任取4个球,红球的个数不比白球少的取法,红球4个,红球3个和白球1个,红球2个和白球2个,
红球4个,取法有1种,
红球3个和白球1个,取法有C43C61=24种;
红球2个和白球2个,取法有C42C62=90种;
根据分类计数原理,红球的个数不比白球少的取法有1+24+90=115种.
(2)使总分不大于6分情况有三种情况,4白,3白1红,2白2红,
第一种,白球4个,取法有C64=15种;
第二种,白球3个和红球1个,取法有C41C63=80种,
第三种,白球2个和红球2个,取法有C42C62=90种,
根据分类计数原理,总分不大于6分的取法有15+80+90=185
红球4个,取法有1种,
红球3个和白球1个,取法有C43C61=24种;
红球2个和白球2个,取法有C42C62=90种;
根据分类计数原理,红球的个数不比白球少的取法有1+24+90=115种.
(2)使总分不大于6分情况有三种情况,4白,3白1红,2白2红,
第一种,白球4个,取法有C64=15种;
第二种,白球3个和红球1个,取法有C41C63=80种,
第三种,白球2个和红球2个,取法有C42C62=90种,
根据分类计数原理,总分不大于6分的取法有15+80+90=185
点评:本题考查组合及组合数公式,考查分类讨论思想,是基础题.

练习册系列答案
相关题目
下边程序运行后,打印输出的结果是( )


| A、-5和-6 | B、1和-8 |
| C、-8和-5 | D、1和-6 |
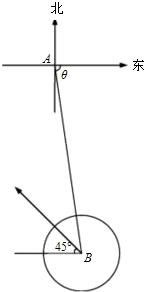 据气象台预报,一台风中心位于某沿海城市A东偏南θ(cosθ=
据气象台预报,一台风中心位于某沿海城市A东偏南θ(cosθ= 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为l的正方形,侧棱AA1=2.
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为l的正方形,侧棱AA1=2.