题目内容
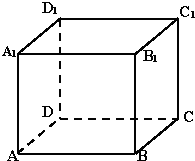 在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是A1B和AC的中点.
在正方体ABCD-A1B1C1D1中,棱长为a,M、N分别是A1B和AC的中点.(1)求异面直线A1B与AC所成角;
(2)求证:MN∥平面BB1C1C.
考点:直线与平面平行的判定,异面直线及其所成的角
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(1)连接A1C1,BC1,证得AA1C1C是平行四边形,得到AC∥A1C1,则∠BA1C1是A1B与AC所成角或其补角,再由
三角形A1BC1是正三角形,即可得到所成的角;
(2)连接AB1,交A1B为M,连接B1C,由中位线定理得到MN∥B1C,再由线面平行的判定定理,即可得证.
三角形A1BC1是正三角形,即可得到所成的角;
(2)连接AB1,交A1B为M,连接B1C,由中位线定理得到MN∥B1C,再由线面平行的判定定理,即可得证.
解答:
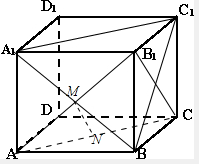 (1)解:连接A1C1,BC1,
(1)解:连接A1C1,BC1,
∵AA1∥BB1,BB1∥CC1,
∴AA1∥CC1,又AA1=CC1,
∴AA1C1C是平行四边形,
∴AC∥A1C1,
∴∠BA1C1是A1B与AC所成角或其补角,
∵A1B=A1C1=BC1,
∴三角形A1BC1是正三角形,
∴∠BA1C1=60°,
∴A1B与AC所成角是60°;
(2)证明:连接AB1,交A1B为M,连接B1C,
在三角形AB1C中,M,N分别为AC,AB1的中点,则MN∥B1C,
∵MN?平面BB1C1C,B1C?平面BB1C1C,
∴MN∥平面BB1C1C.
 (1)解:连接A1C1,BC1,
(1)解:连接A1C1,BC1,∵AA1∥BB1,BB1∥CC1,
∴AA1∥CC1,又AA1=CC1,
∴AA1C1C是平行四边形,
∴AC∥A1C1,
∴∠BA1C1是A1B与AC所成角或其补角,
∵A1B=A1C1=BC1,
∴三角形A1BC1是正三角形,
∴∠BA1C1=60°,
∴A1B与AC所成角是60°;
(2)证明:连接AB1,交A1B为M,连接B1C,
在三角形AB1C中,M,N分别为AC,AB1的中点,则MN∥B1C,
∵MN?平面BB1C1C,B1C?平面BB1C1C,
∴MN∥平面BB1C1C.
点评:本题考查空间直线与平面平行的判定定理和空间两异面直线所成的角的求法,注意运用平面几何中的有关定理,本题属于中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
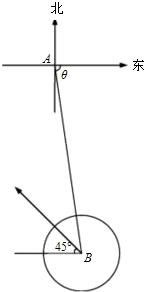 据气象台预报,一台风中心位于某沿海城市A东偏南θ(cosθ=
据气象台预报,一台风中心位于某沿海城市A东偏南θ(cosθ= 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为l的正方形,侧棱AA1=2.
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为l的正方形,侧棱AA1=2.