题目内容
已知tan（3π+α）=-3，求：
（1）tan（
+α）；
（2）4sin2α-3sinαcosα．
（1）tan（
| π |
| 4 |
（2）4sin2α-3sinαcosα．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）已知等式左边利用诱导公式化简求出tanα的值，原式利用两角和与差的正切函数公式化简，把tanα的值代入计算即可求出值；
（2）原式利用同角三角函数间基本关系变形，把tanα的值代入计算即可求出值．
（2）原式利用同角三角函数间基本关系变形，把tanα的值代入计算即可求出值．
解答：
解：（1）∵tan（3π+α）=tanα=-3，
∴tan（
+α）=
=
=-
；
（2）∵tanα=-3，
∴原式=
=
=
=
．
∴tan（
| π |
| 4 |
| tanα+1 |
| 1-tanα |
| -3+1 |
| 1+3 |
| 1 |
| 2 |
（2）∵tanα=-3，
∴原式=
| 4sin2α-3sinαcosα |
| sin2α+cos2α |
| 4tan2α-3tanα |
| tan2α+1 |
| 4×(-3)2-3(-3) |
| (-3)2+1 |
| 9 |
| 2 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
已知椭圆两条准线间的距离是焦距的2倍，则其离心率为（ ）
A、
| ||||
B、
| ||||
| C、6 | ||||
| D、2 |
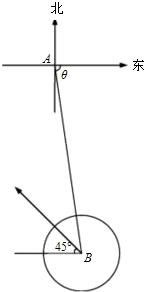据气象台预报，一台风中心位于某沿海城市A东偏南θ（cosθ=