题目内容
已知函数f(x)=x2-alnx-x(a≠0).
(1)求函数f(x)的单调区间;
(2)若a>0,设A(x1,y1),B(x2,y2)是函数f(x)图象上的任意两点(x1<x2),记直线AB的斜率为k,求证:f′(
)>k.
(1)求函数f(x)的单调区间;
(2)若a>0,设A(x1,y1),B(x2,y2)是函数f(x)图象上的任意两点(x1<x2),记直线AB的斜率为k,求证:f′(
| x1+2x2 |
| 3 |
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)先求导,再根据a的值进行分类讨论,得到函数的单调区间.
(2)先求导,根据题意,由直线的斜率公式可得k的值,利用分析法证明f′(
)>k.转化为只需要证明
>
,再构造函数g(t),判断函数在(0,1)上单调性,问题得以证明
(2)先求导,根据题意,由直线的斜率公式可得k的值,利用分析法证明f′(
| x1+2x2 |
| 3 |
ln
| ||
| x1-x2 |
| 3 |
| x1+2x2 |
解答:
解:(1)f′(x)=2x-
-1=
(x>0)
(i)当a≤-
时,2x2-x-a≥0 恒成立,即f'(x)≥0恒成立,
故函数f(x)的单增区间为(0,+∞),无单减区间.
(ii)当-
<a<0时,f′(x)>0⇒2x2-x-a>0,
解得:x>
或x<
∵x>0,∴函数f(x)的单增区间为(0,
),(
,+∞),
单减区间为(
,
).
(iii)当a>0时,由f′(x)>0解得:x>
或x<
.
∵x>0,而此时
<0,∴函数f(x)的单增区间为(
,+∞),
单减区间为(0,
).
综上所述:
(i)当a≤-
时,f(x)的单增区间为(0,+∞),无单减区间.
(ii)当-
<a<0时,f(x)的单增区间为(0,
),(
,+∞),
单减区间为(
,
).
(iii)当a>0时,f(x)的单增区间为(
,+∞),单减区间为(0,
).
(2)证明:∵f′(x)=2x-
-1
∴f′(
)=
-
-1
由题意得,k=
=
=(x1+x2)-
-1
则:f′(
)-k=
-(x1+x2)-
+
=
-
+
注意到
>0,
故欲证f′(
)>k,
只须证明:
>
.
因为a>0,故即证:
>
令
=t∈(0,1),g(t)=lnt-
则:g′(t)=
-
=
>0
故g(t)在(0,1)上单调递增.
即:lnt<
,
即:ln
<
所以:f′(
)>k.
| a |
| x |
| 2x2-x-a |
| x |
(i)当a≤-
| 1 |
| 8 |
故函数f(x)的单增区间为(0,+∞),无单减区间.
(ii)当-
| 1 |
| 8 |
解得:x>
1+
| ||
| 4 |
1-
| ||
| 4 |
∵x>0,∴函数f(x)的单增区间为(0,
1-
| ||
| 4 |
1+
| ||
| 4 |
单减区间为(
1-
| ||
| 4 |
1+
| ||
| 4 |
(iii)当a>0时,由f′(x)>0解得:x>
1+
| ||
| 4 |
1-
| ||
| 4 |
∵x>0,而此时
1-
| ||
| 4 |
1+
| ||
| 4 |
单减区间为(0,
1+
| ||
| 4 |
综上所述:
(i)当a≤-
| 1 |
| 8 |
(ii)当-
| 1 |
| 8 |
1-
| ||
| 4 |
1+
| ||
| 4 |
单减区间为(
1-
| ||
| 4 |
1+
| ||
| 4 |
(iii)当a>0时,f(x)的单增区间为(
1+
| ||
| 4 |
1+
| ||
| 4 |
(2)证明:∵f′(x)=2x-
| a |
| x |
∴f′(
| x1+2x2 |
| 3 |
| 2(x1+2x2) |
| 3 |
| 3a |
| x1+2x2 |
由题意得,k=
| y1-y2 |
| x1-x2 |
| (x1 2-x2 2)-a(lnx1-lnx2)-(x1-x2) |
| x1-x2 |
aln
| ||
| x1-x2 |
则:f′(
| x1+2x2 |
| 3 |
| 2(x1+2x2) |
| 3 |
| 3a |
| x1+2x2 |
aln
| ||
| x1-x2 |
| x2-x1 |
| 3 |
| 3a |
| x1+2x2 |
aln
| ||
| x1-x2 |
注意到
| x2-x1 |
| 3 |
故欲证f′(
| x1+2x2 |
| 3 |
只须证明:
aln
| ||
| x1-x2 |
| 3a |
| x1+2x2 |
因为a>0,故即证:
ln
| ||
| x1-x2 |
| 3 |
| x1+2x2 |
令
| x1 |
| x2 |
| 3(t-1) |
| t+2 |
则:g′(t)=
| 1 |
| t |
| 9 |
| (t+2)2 |
| (t-1)(t-4) |
| t(t+2)2 |
故g(t)在(0,1)上单调递增.
即:lnt<
| 3(t-1) |
| t+2 |
即:ln
| x1 |
| x2 |
3(
| ||
|
所以:f′(
| x1+2x2 |
| 3 |
点评:本题考查导数的应用,涉及斜率,最大值、最小值的求法,是综合题;关键是理解导数的符号与单调性的关系,并能正确求出函数的导数,属于难题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
下边程序运行后,打印输出的结果是( )


| A、-5和-6 | B、1和-8 |
| C、-8和-5 | D、1和-6 |
等比数列{an}各项为正数,且a2a4+a4a6+2a3a5=9,则a3+a5的值为( )
| A、3 | B、6 | C、9 | D、12 |
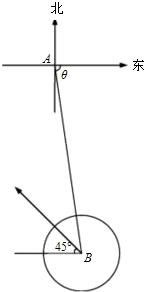 据气象台预报,一台风中心位于某沿海城市A东偏南θ(cosθ=
据气象台预报,一台风中心位于某沿海城市A东偏南θ(cosθ= 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为l的正方形,侧棱AA1=2.
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面ABCD是边长为l的正方形,侧棱AA1=2.