题目内容
由于某种商品开始收税，使其定价比原定价上涨x成（即上涨率为
），涨价后商品卖出的个数减少bx成，税率是新价的a成，这里a，b均为常数，且a＜10，用A表示过去定价，B表示过去卖出的个数．
（1）设售货款扣除税款后，剩余y元，求y关于x的函数解析式；
（2）要使y最大，求x的值．
| x |
| 10 |
（1）设售货款扣除税款后，剩余y元，求y关于x的函数解析式；
（2）要使y最大，求x的值．
考点：导数在最大值、最小值问题中的应用
专题：导数的综合应用
分析：（1）定价上涨x成，即为A（1+
），卖出的个数为B（1-
），售货款扣除税款后，能求出y关于x的函数解析式．
（2）由已知得y′=AB(1-
)(-
x+
-
)，由此利用导数性质能求出使y最大的x的值．
| x |
| 10 |
| bx |
| 10 |
（2）由已知得y′=AB(1-
| a |
| 10 |
| b |
| 50 |
| 1 |
| 10 |
| b |
| 10 |
解答：
解：（1）定价上涨x成，即为A（1+
），
卖出的个数为B（1-
），售货款扣除税款后，
剩余y=AB（1+
）（1-
）（1-
），（0＜x＜10）．
（2）y=AB（1+
）（1-
）（1-
）
=AB（1-
）[-
x2+（
-
）x+1]，
∴y′=AB(1-
)(-
x+
-
)，
令y′=0，得x=
，
x∈（0，
）时，y′＞0；当x∈（
，10）时，y′＜0．
∴ymax=y|x=
=AB（1-
）•
．
∴使y最大有x的值为
．
| x |
| 10 |
卖出的个数为B（1-
| bx |
| 10 |
剩余y=AB（1+
| x |
| 10 |
| bx |
| 10 |
| a |
| 10 |
（2）y=AB（1+
| x |
| 10 |
| bx |
| 10 |
| a |
| 10 |
=AB（1-
| a |
| 10 |
| b |
| 100 |
| 1 |
| 10 |
| b |
| 10 |
∴y′=AB(1-
| a |
| 10 |
| b |
| 50 |
| 1 |
| 10 |
| b |
| 10 |
令y′=0，得x=
| 5(1-b) |
| b |
x∈（0，
| 5(1-b) |
| b |
| 5(1-b) |
| b |
∴ymax=y|x=
| 5(1-b) |
| b |
| a |
| 10 |
| (1+b)2 |
| 4b |
∴使y最大有x的值为
| 5(1-b) |
| b |
点评：本题考查函数的解析式的求法，考查要使y最大，x的值的求法，解题时要认真审题，注意导数性质的合理运用．
练习册系列答案
期末集结号系列答案
相关题目
已知 cosx=-
，其中x∈（π，2π），则x等于（ ）
| 1 |
| 3 |
A、π+arccos
| ||
B、π-arccos
| ||
C、π+arccos（-
| ||
D、2π-arccos
|
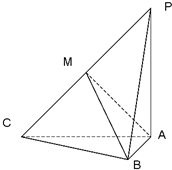如图，三棱锥P-ABC中，