题目内容
已知tanα=3，计算：（1）
；（2）sin2θ+7sinθcosθ的值．
| 4sinα-2cosα |
| 5cosα+3sinα |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）原式分子分母除以cosα，利用同角三角函数间基本关系化简，把tanα的值代入计算即可求出值；
（2）原式分母看做“1”，利用同角三角函数间基本关系化简，把tanα的值代入计算即可求出值．
（2）原式分母看做“1”，利用同角三角函数间基本关系化简，把tanα的值代入计算即可求出值．
解答：
解：（1）∵tanα=3，
∴原式=
=
=
；
（2）∵tanα=3，
∴原式=
=
=
=3．
∴原式=
| 4tanα-2 |
| 5+3tanα |
| 12-2 |
| 5+9 |
| 5 |
| 7 |
（2）∵tanα=3，
∴原式=
| sin2θ+7sinθcosθ |
| sin2θ+cos2θ |
| tan2θ+7tanθ |
| tan2θ+1 |
| 9+21 |
| 9+1 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知an=3-2n，则数列{an}为（ ）
| A、首项为3的等差数列 |
| B、公差为3的等差数列 |
| C、公差为-2的等差数列 |
| D、公差为-2n的等差数列 |
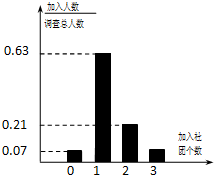为了丰富学校课余文化生活，锻炼学生的综合能力，浏阳一中成立了多个学生社团，并鼓励学生参加社团活动或加入社团组织经过调研，若学生人均加入社团1～2个，则说明社团活动开展得有序．为此，学校规定学生加入的社团个数不能超过3个．社团文化节期间，校团委为了了解学生社团活动开展情况，随机发放并回收了100份调查问卷，并对各项指标进行了统计，其中学生参加社团的个数情况统计如图所示．