题目内容
已知函数f(x)=asin3x+bx3+4(a∈R,b∈R),f′(x)为f(x)的导函数,则f(2014)+f(-2014)+f′(2015)-f′(-2015)=( )
| A、8 | B、2014 |
| C、2015 | D、0 |
考点:导数的运算
专题:函数的性质及应用,导数的概念及应用
分析:观察已知解析式f(x)=asin3x+bx3+4,构造g(x)=f(x)-4=asin3x+bx3是奇函数,而它的导数是偶函数,利用奇偶函数的性质解答.
解答:
解:由已知,设函数g(x)=f(x)-4=asin3x+bx3是奇函数,由g(-x)=-g(x),∴g(x)为奇函数,
f′(x)=3acos3x+3bx2为偶函数,∴f′(-x)=f′(x),
∴f(2014)+f(-2014)+f′(2015)-f′(-2015)=g(2014)+4+g(-2014)+4+f′(2015)-f′(2015)=g(2014)-g(2014)+f′(2015)-f′(2015)+8=8.
故选A.
f′(x)=3acos3x+3bx2为偶函数,∴f′(-x)=f′(x),
∴f(2014)+f(-2014)+f′(2015)-f′(-2015)=g(2014)+4+g(-2014)+4+f′(2015)-f′(2015)=g(2014)-g(2014)+f′(2015)-f′(2015)+8=8.
故选A.
点评:本题考查了导数的运算以及函数奇偶性的运用,灵活构造函数g(x)是解答本题的关键.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
函数y=
的导数是( )
| 1 |
| x |
| A、y'=ex | ||
| B、y'=lnx | ||
C、y′=
| ||
| D、y'=-x-2 |
下列函数中,值域是(0,+∞)的函数是( )
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=(
|
y=2x+1在[1,2]内的平均变化率为( )
| A、3 | B、2 | C、1 | D、0 |
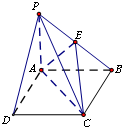 在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4
在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4