题目内容
4．已知直线x+2ay-1=0与直线x-4y=0平行，则a的值为（ ）| A． | -2 | B． | 2 | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
分析 利用两条直线平行，它们的斜率相等求解．
解答 解：∵直线x+2ay-1=0与直线x-4y=0平行，
∴-$\frac{1}{2a}$=$\frac{1}{4}$，
解得a=-2．
故选：A
点评 本题考查实数值的求法，是基础题，解题时要认真审题，注意两直线平行的性质的合理运用．
练习册系列答案
相关题目
15．已知F是抛物线x2=y的焦点，A，B是该抛物线上的两点，|AF|+|BF|=3，则线段AB的中点到x轴的距离为（ ）
| A． | $\frac{3}{4}$ | B． | 1 | C． | $\frac{5}{4}$ | D． | $\frac{7}{4}$ |
12．函数f（x）=sinxcosx-cos2x+$\frac{1}{2}$在区间[0，$\frac{π}{2}$]上的最小值是（ ）
| A． | -1 | B． | -$\frac{1}{2}$ | C． | 1 | D． | 0 |
16．已知a=cos17°cos23°-sin17°sin23°，b=2cos225°-1，c=$\frac{{\sqrt{3}}}{2}$，则a，b，c的大小关系（ ）
| A． | b＞a＞c | B． | c＞b＞a | C． | c＞a＞b | D． | a＞c＞b |
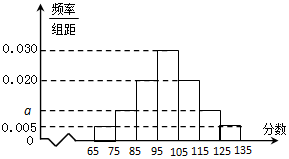某校高二年级在一次数学测验后，随机抽取了部分学生的数学成绩组成一个样本，得到如下频率分布直方图：