题目内容
12.函数f(x)=sinxcosx-cos2x+$\frac{1}{2}$在区间[0,$\frac{π}{2}$]上的最小值是( )| A. | -1 | B. | -$\frac{1}{2}$ | C. | 1 | D. | 0 |
分析 把函数解析式利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式积特殊角的三角函数值化为一个角的正弦函数,由x的范围求出这个角的范围,利用正弦函数的图象与性质即可求出f(x)在区间[0,$\frac{π}{2}$]上的最小值
解答 解:∵f(x)=sinxcosx-cos2x+$\frac{1}{2}$=$\frac{1}{2}$sin2x-$\frac{1}{2}$cos2x=$\frac{\sqrt{2}}{2}$sin(2x-$\frac{π}{4}$)
∴当x∈[0,$\frac{π}{2}$]时,
∴-$\frac{π}{4}$≤2x-$\frac{π}{4}$≤$\frac{3π}{4}$,
∴当2x-$\frac{π}{4}$=-$\frac{π}{4}$时,
函数$f(x)=\frac{{\sqrt{2}}}{2}sin(2x-\frac{π}{4})$的最小值为$-\frac{1}{2}$,
故选B.
点评 此题考查了二倍角的正弦、余弦函数公式,两角和与差的正弦函数公式,以及正弦函数的图象与性质,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
3.若0<x1<x2<1,则( )
| A. | ${x_2}{e^{x_1}}>{x_1}{e^{x_2}}$ | B. | ${x_2}{e^{x_1}}<{x_1}{e^{x_2}}$ | ||
| C. | lnx2-lnx1>2x2-2x1 | D. | lnx2-lnx1<2x2-2x1 |
7.已知角α的终边经过点(-4,-3),那么tanα等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{4}{3}$ |
4.已知直线x+2ay-1=0与直线x-4y=0平行,则a的值为( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
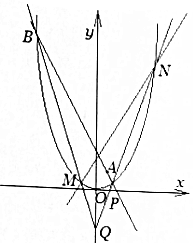 已知过点P($\frac{1}{2}$,0)的直线l与抛物线x2=y交于不同的两点A,B,点Q(0,-1),连接AQ、BQ的直线与抛物线的另一交点分别为N,M,如图所示.
已知过点P($\frac{1}{2}$,0)的直线l与抛物线x2=y交于不同的两点A,B,点Q(0,-1),连接AQ、BQ的直线与抛物线的另一交点分别为N,M,如图所示.