题目内容
14. 某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:
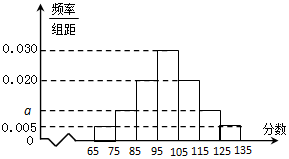
某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:(1)求a及这部分学生成绩的样本平均数$\overline x$(同一组数据用该组的中点值作为代表);
(2)若该校高二共有1000名学生,试估计这次测验中,成绩在105分以上的学生人数.
分析 (1)由频率和为1列出方程求出a的值,再计算平均数;
(2)由频率分布直方图计算学生成绩在105分以上的频率与频数.
解答 解:(1)由频率分布直方图可知:
(0.005×2+2a+0.020×2+0.030)×10=1,
∴a=0.010;…(3分)
平均数为$\overline{x}$=(70×0.005+80×0.010+90×0.020+100×0.030
+110×0.020+120×0.010+130×0.005)×10=100分;…(7分)
(2)由频率分布直方图可知:
学生成绩在105分以上的频率为
(0.020+0.010+0.005)×10=0.35;
∴该校高二1000名学生中,数学成绩在105分以上的大约有
1000×0.35=350人.…(12分)
点评 本题考查了频率分布直方图与频率、频数、平均数的计算问题,是基础题目.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
4.已知直线x+2ay-1=0与直线x-4y=0平行,则a的值为( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
9.袋中装有红球3个、白球2个、黑球1个,从中任取2个,则互斥而不对立的两个事件是( )
| A. | 至少有一个白球;至少有一个红球 | B. | 至少有一个白球;红、黑球各一个 | ||
| C. | 恰有一个白球;一个白球一个黑球 | D. | 至少有一个白球;都是白球 |
6.已知$|{\vec a}|=1$,$|{\vec b}|=2$,$\vec a(\vec a-\vec b)=3$则$\vec a$与$\vec b$的夹角为( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{2}$ | D. | π |
3.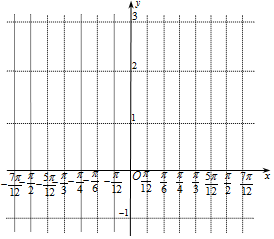 某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:
某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:
(1)请将上表数据补充完整,并在给出的直角坐标系中,画出f(x)在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象;
(2)求f(x)的最小值及取最小值时x的集合;
(3)求f(x)在$x∈[0,\frac{π}{2}]$时的值域.
 某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:
某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:| 2x-$\frac{π}{3}$ | -$\frac{4}{3}$π | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | $\frac{2}{3}$π |
| x | -$\frac{π}{2}$ | -$\frac{π}{3}$ | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{π}{2}$ |
| f(x) |
(2)求f(x)的最小值及取最小值时x的集合;
(3)求f(x)在$x∈[0,\frac{π}{2}]$时的值域.
4.设x∈R,则“1<x<3”是“|x-2|<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
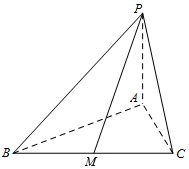 在三棱锥P-ABC中,底面ABC是边长为6的正三角形,PA⊥底面ABC,且PB与底面ABC所成的角为$\frac{π}{6}$.
在三棱锥P-ABC中,底面ABC是边长为6的正三角形,PA⊥底面ABC,且PB与底面ABC所成的角为$\frac{π}{6}$.