题目内容

若
a
=（m，4）（m＞0），且|
a
|=5，则m的值是
 
．
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：由模长公式可得m的方程，解方程结合m＞0可得．
解答： 解：∵
a
=（m，4），
∴|
a
|=
m2+42
=5，
即m2+16=25，
解得m=3或m=-3，
∵m＞0，∴m=3
故答案为：3
点评：本题考查向量的模长公式，属基础题．
练习册系列答案
相关题目
已知函数f（x）=
x2+ax+a
x
，x∈[1，+∞）且a＜1
（1）判断f（x）的单调性并证明；
（2）若m满足f（3m）＞f（5-2m），试确定m的取值范围．
（3）若函数g（x）=x•f（x）对任意x∈[2，5]时，g（x）+2x+
3
2
＞0恒成立，求a的取值范围．
求下列各圆的标准方程：
（1）圆心在y=-x上且过两点（2，0），（0，-4）；
（2）圆心在直线5x-3y=8上，且与坐标轴相切．
下列各组函数f（x）与g（x）的图象相同的是（　　）
A、f（x）=x，g（x）=（
x
）2
B、f（x）=x2，g（x）=（x+1）2
C、f（x）=1，g（x）=
x
x
D、f（x）=|x|，g（x）=
x
-x
(x≥0)
(x＜0)
已知以F为焦点的抛物线y2=4x上的两点A、B满足
AF
=3
FB
，则弦AB的中点到准线的距离为（　　）
A、
8
3
B、
4
3
C、2
D、1
在直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴建立极坐标系，已知圆C的圆心的极坐标为（
2
，
π
4
），半径r=
2
，点P的极坐标为（2，π），过P作直线l交圆C于A，B两点．
（1）求圆C的直角坐标方程；
（2）求|PA|•|PB|的值．
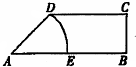一只受伤的丹顶鹤在如图所示（直角梯形）的草原上飞过，其中AD=
2
，DC=2，BC=1，它可能随机在草原上任何一处（点），若落在扇形沼泽区域ADE以外丹顶鹤能生还，则该丹顶鹤生还的概率是（　　）
A、
1
2
-
π
15
B、1-
π
10
C、1-
π
6
D、1-
3π
10
已知函数f（x）=
a
3
x3+ax2+cx，g(x)=ax2+2ax+c，a≠0，则它们的图象可能是（　　）
A、
B、
C、
D、
在△ABC中，A，B，C所对的边分别为a，b，c，向量
m
=(cosA，sinA)，向量
n
=(
2
-sinA，cosA)
若|
m
+
n
|=2．
（1）求角A的大小；
（2）若△ABC外接圆的半径为2，b=2，求边c的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网