题目内容
已知以F为焦点的抛物线y2=4x上的两点A、B满足
=3
，则弦AB的中点到准线的距离为（ ）
| AF |
| FB |
A、
| ||
B、
| ||
| C、2 | ||
| D、1 |
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：设BF=m，由抛物线的定义知AA1和BB1，进而可推断出AC和AB，及直线AB的斜率，则直线AB的方程可得，与抛物线方程联立消去y，进而跟韦达定理求得x1+x2的值，则根据抛物线的定义求得弦AB的中点到准线的距离．
解答：
解：设BF=m，由抛物线的定义知
AA1=3m，BB1=m，
∴△ABC中，AC=2m，AB=4m，kAB=
，
直线AB方程为y=
（x-1），
与抛物线方程联立消y得3x2-10x+3=0，
所以AB中点到准线距离为
+1=
+1=
．
故选A．
AA1=3m，BB1=m，
∴△ABC中，AC=2m，AB=4m，kAB=
| 3 |
直线AB方程为y=
| 3 |
与抛物线方程联立消y得3x2-10x+3=0，
所以AB中点到准线距离为
| x1+x2 |
| 2 |
| 5 |
| 3 |
| 8 |
| 3 |
故选A．
点评：本题主要考查了抛物线的简单性质．考查了直线与抛物线的关系及焦点弦的问题．常需要利用抛物线的定义来解决．
练习册系列答案
相关题目
已知圆M：x2+y2-2y=24，直线l：x+y=11，l上一点A的横坐标为a，过点A作圆M的两条切线l1，l2切点分别为B，C．
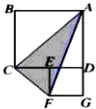如图，点E在正方形ABCD边CD上，四边形DEFG也是正方形，已知AB=a，DE=b（a，b为常数，且a＞b＞0），则△ACF的面积（ ）| A、只与a的大小有关 |
| B、只与b的大小有关 |
| C、只与CE的大小有关 |
| D、无法确定 |
已知三个实数a=0.76，b=60.7，c=log
，则a，b，c的大小关系正确的为（ ）
6 0.7 |
| A、a＜b＜c |
| B、a＜c＜b |
| C、c＜a＜b |
| D、c＜b＜a |
已知集合M={x|x=1+a2，a∈N*}，P={x|x=a2-2a+2，a∈N*}，则集合M与P的关系是（ ）
| A、M?P | B、P?M |
| C、M=P | D、M?P且P?M |