题目内容

18．以（1，-1）为中点的抛物线y2=8x的弦所在直线的方程存在吗？若存在，求出直线方程；若不存在，请说明理由．

分析 先设出弦的两端点的坐标然后代入到抛物线方程后两式相减，可求得直线方程的斜率，最后根据直线的点斜式可求得方程．

解答 解：设这样的直线存在，其被抛物线截得弦的两端点分别为A（x1，y1），B（x2，y2），
则yi2=8x1，y22=8x2  ①…（2分）
①中两式做差，得（y2+y1）（y2-y1）=8（x2-x1），
∴kAB=-4．…（12分）
得直线方程 y+1=-4（x-1），即4x+y-3=0．②…（14分）
将②与曲线y2=8x联立，
得16x2-32x+9=0，△=（-32）2-4×16×9＞0（必须检验！） …（15分）
∴弦所在直线方程为4x+y-3=0．…（16分）

点评 本题主要考查直线和抛物线的综合问题，考查综合运用能力．

练习册系列答案
相关题目
8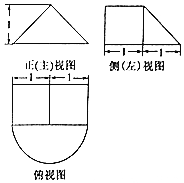．一个由半圆锥和平放的直三棱柱（侧棱垂直于底面的三棱柱）组成的几何体，其三视图如图所示，则该几何体的体积为（　　）
A．1+$\frac{π}{3}$B．1+$\frac{π}{6}$C．$\frac{2}{3}$+$\frac{π}{3}$D．$\frac{2}{3}$+$\frac{π}{6}$
9．计算：已知角α终边上的一点P（7m，-3m）（m≠0）．
（Ⅰ）求$\frac{cos（\frac{π}{2}+α）sin（-π-α）}{cos（\frac{11π}{2}-α）sin（\frac{9π}{2}+α）}$的值；
（Ⅱ）求2+sinαcosα-cos2α的值．
6．设函数$f（x）={x^2}+\frac{1}{x+1}，x∈[0，1]$．
（1）证明：$f（x）≥{x^2}-\frac{4}{9}x+\frac{8}{9}$；
（2）证明：$\frac{68}{81}＜f（x）≤\frac{3}{2}$．
13．下列选项中，说法正确的是（　　）
A．若命题“p或q”为真命题，则命题p和命题q均为真命题
B．命题“若am2＜bm2，则a＜b”的逆命题是真命题
C．命题“若a=-b，则|a|=|b|”的否命题是真命题
D．命题“若$\left\{{\overrightarrow a，\overrightarrow b，\overrightarrow c}\right\}$为空间的一个基底，则$\left\{{\overrightarrow a+\overrightarrow b，\overrightarrow b+\overrightarrow c，\overrightarrow c+\overrightarrow a}\right\}$构成空间的另一个基底”的逆否命题为真命题
3．函数f（x）=2x2-lnx的递增区间是（　　）
A．$（0，\frac{1}{2}）$B．$（-\frac{1}{2}，0）$和$（\frac{1}{2}，+∞）$C．$（\frac{1}{2}，+∞）$D．$（-∞，-\frac{1}{2}）$和$（0，\frac{1}{2}）$
10．经过点A（-1，4）且在x轴上的截距为3的直线方程是（　　）
A．x+y+3=0B．x-y+3=0C．x+y-3=0D．x-y-3=0
7．已知函数f（x）=x+a，g（x）=x+$\frac{4}{x}$，若?x1∈[1，3]，?x2∈[1，4]，使得f（x1）≥g（x2），则实数a的取值范围为（　　）
A．a≥1B．a≥2C．a≥3D．a≥4
8．已知函数f（x）=x3-3x2，g（x）=ax2-4．
（Ⅰ）求函数f（x）的极值；
（Ⅱ）若对任意的x∈[0，+∞），都有f（x）≥g（x），求实数a的取值范围；
（Ⅲ）函数f（x）的图象是否为中心对称图形，如果是，请写出对称中心；如果不是，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网