题目内容
6.设函数$f(x)={x^2}+\frac{1}{x+1},x∈[0,1]$.(1)证明:$f(x)≥{x^2}-\frac{4}{9}x+\frac{8}{9}$;
(2)证明:$\frac{68}{81}<f(x)≤\frac{3}{2}$.
分析 (1)令g(x)=f (x)-x2+$\frac{4}{9}$x-$\frac{8}{9}$,化简求导,判断g(x)的单调性,求出最值即可得到结果.
(2)求出导数,设h(x)=2x3+4x2+2x-1,求出h′(x)求出 f (x)max,结合(1)推出结果.
解答 (本题满分15分)
证明:(1)令g(x)=f (x)-x2+$\frac{4}{9}$x-$\frac{8}{9}$,即g(x)=$\frac{1}{x+1}$+$\frac{4}{9}$x-$\frac{8}{9}$,
所以$g'(x)=\frac{{4{x^2}+8x-5}}{{9{{(x+1)}^2}}}=\frac{(2x-1)(2x+5)}{{9{{(x+1)}^2}}}$,
所以g(x)在$({0,\frac{1}{2}})$上递减,在$({\frac{1}{2},1})$上递增,
所以g(x)≥$g({\frac{1}{2}})$=0,所以f (x)≥x2-$\frac{4}{9}$x+$\frac{8}{9}$. …(7分)
(2)因为$f'(x)=\frac{{2{x^3}+4{x^2}+2x-1}}{{{{(x+1)}^2}}}$,x∈[0,1],
设h(x)=2x3+4x2+2x-1,h′(x)=6x2+8x+2,
因为h(0)=-1,h(1)=7,
所以存在x0∈(0,1),使得f′(x)=0,且f (x)在(0,x0)上递减,在(x0,1)上递增,
所以 f (x)max={ f (0),f (1)}=f (1)=$\frac{3}{2}$.
由(1)知,f (x)≥x2-$\frac{4}{9}$x+$\frac{8}{9}$=${({x-\frac{2}{9}})^2}+\frac{68}{81}$≥$\frac{68}{81}$,
又$f({\frac{1}{2}})$=$\frac{11}{12}$$>\frac{68}{81}$,$f({\frac{2}{9}})=\frac{773}{891}>\frac{68}{81}$,
所以$\frac{68}{81}$<f (x)≤$\frac{3}{2}$. …(8分)
点评 本题考查函数的导数的应用,函数的单调性以及函数的最值的求法,考查转化思想以及计算能力.

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案| A. | (0,3) | B. | [0,3) | C. | (0,3] | D. | [0,3] |
| ξ | -1 | 0 | 1 | 2 |
| P | x | $\frac{1}{3}$ | $\frac{1}{6}$ | y |
| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
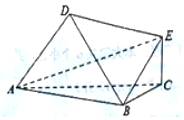 如图,以A,B,C,D,E为顶点的六面体中,△ABC和△ABD均为正三角形,且平面ABC⊥平面ABD,EC⊥面ABC,EC=$\frac{{\sqrt{3}}}{2}$,AB=2.
如图,以A,B,C,D,E为顶点的六面体中,△ABC和△ABD均为正三角形,且平面ABC⊥平面ABD,EC⊥面ABC,EC=$\frac{{\sqrt{3}}}{2}$,AB=2.