题目内容
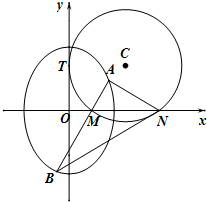 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的左侧),且|MN|=3.
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的左侧),且|MN|=3.(Ⅰ)求圆C的方程;
(Ⅱ)过点M任作一条直线与椭圆Γ:
| x2 |
| 4 |
| y2 |
| 8 |
AN、BN,求证:∠ANM=∠BNM.
考点:直线和圆的方程的应用
专题:计算题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)设圆C的半径为r(r>0),由|MN|=3可得r2=(
)2+22,从而求圆C的方程;
(Ⅱ)求出点M(1,0),N(4,0),讨论当AB⊥x轴时与AB与x轴不垂直时∠ANM是否相等∠BNM,从而证明.
| 3 |
| 2 |
(Ⅱ)求出点M(1,0),N(4,0),讨论当AB⊥x轴时与AB与x轴不垂直时∠ANM是否相等∠BNM,从而证明.
解答:
解:(Ⅰ)设圆C的半径为r(r>0),则圆心坐标为(r,2).
∵|MN|=3,
∴r2=(
)2+22,解得r2=
.
∴圆C的方程为(x-
)2+(y-2)2=
.
(Ⅱ)证明:把y=0代入方程(x-
)2+(y-2)2=
,解得x=1,或x=4,
即点M(1,0),N(4,0).
(1)当AB⊥x轴时,由椭圆对称性可知∠ANM=∠BNM.
(2)当AB与x轴不垂直时,可设直线AB的方程为y=k(x-1).
联立方程
,消去y得,(k2+2)x2-2k2x+k2-8=0.
设直线AB交椭圆Γ于A(x1,y1)、B(x2,y2)两点,则x1+x2=
,x1•x2=
.
∵y1=k(x1-2),y2=k(x2-2),
∴kAN+kBN=
+
=
+
=
.
∵(x1-1)(x2-4)+(x2-1)(x1-4)=2x1x2-5(x1+x2)+8=
-
+8=0,
∴kAN+kBN=0,∠ANM=∠BNM.
综上所述,∠ANM=∠BNM.
∵|MN|=3,
∴r2=(
| 3 |
| 2 |
| 25 |
| 4 |
∴圆C的方程为(x-
| 5 |
| 2 |
| 25 |
| 4 |
(Ⅱ)证明:把y=0代入方程(x-
| 5 |
| 2 |
| 25 |
| 4 |
即点M(1,0),N(4,0).
(1)当AB⊥x轴时,由椭圆对称性可知∠ANM=∠BNM.
(2)当AB与x轴不垂直时,可设直线AB的方程为y=k(x-1).
联立方程
|
设直线AB交椭圆Γ于A(x1,y1)、B(x2,y2)两点,则x1+x2=
| 2k2 |
| k2+2 |
| k2-8 |
| k2+2 |
∵y1=k(x1-2),y2=k(x2-2),
∴kAN+kBN=
| y1 |
| x1-4 |
| y2 |
| x2-4 |
| k(x1-1) |
| x1-4 |
| k(x2-1) |
| x2-4 |
| k(x1-1)(x2-4)+k(x2-1)(x1-4) |
| (x1-4)(x2-4) |
∵(x1-1)(x2-4)+(x2-1)(x1-4)=2x1x2-5(x1+x2)+8=
| 2(k2-8) |
| k2+2 |
| 10k2 |
| k2+2 |
∴kAN+kBN=0,∠ANM=∠BNM.
综上所述,∠ANM=∠BNM.
点评:本题考查了圆的方程的求法及圆锥曲线与直线的交点问题,化简比较复杂,通过根与系数的关系简化运算,要细心,属于中档题.

练习册系列答案
相关题目
对命题p:1∈{1},命题q:1∉∅,下列说法正确的是( )
| A、p且q为假命题 |
| B、p或q为假命题 |
| C、非p为真命题 |
| D、非q为假命题 |
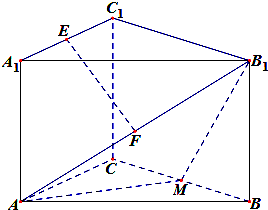 在正三棱柱ABC-A1B1C1中,BC=
在正三棱柱ABC-A1B1C1中,BC=