题目内容
设a∈R,函数f(x)=
x3-
(2a+1)x2+(a2+a)x.
(Ⅰ)已知f′(x)是f(x)的导函数,且g(x)=
(x≠0)为奇函数,求a的值;
(Ⅱ)若函数f(x)在x=2处取得极小值,求函数f(x)的单调递增区间.
| 1 |
| 3 |
| 1 |
| 2 |
(Ⅰ)已知f′(x)是f(x)的导函数,且g(x)=
| f′(x) |
| x |
(Ⅱ)若函数f(x)在x=2处取得极小值,求函数f(x)的单调递增区间.
考点:利用导数研究函数的单调性,函数奇偶性的性质
专题:计算题,函数的性质及应用,导数的综合应用
分析:(Ⅰ)求出函数f(x)的导数f'(x),得到g(x)的表达式,再由奇函数的定义,即可得到a;
(Ⅱ)求出f(x)的导数,求出单调区间,得到极值,令极小值点为2,解出a,进而得到单调增区间.
(Ⅱ)求出f(x)的导数,求出单调区间,得到极值,令极小值点为2,解出a,进而得到单调增区间.
解答:
解:(Ⅰ)f'(x)=x2-(2a+1)x+(a2+a),
故 g(x)=
=x+
-(2a+1),x≠0,
∵g(x)=
(x≠0)为奇函数,
∴?x≠0,g(-x)+g(x)=0,即2a+1=0,
∴a=-
;
(Ⅱ)f'(x)=x2-(2a+1)x+(a2+a)=(x-a)[x-(a+1)],
列表如下:
∴f(x)在x=a+1处取得极小值,在x=a处取得极大值,
由题设a+1=2,∴a=1;
所以函数的递增区间为(-∞,1),(2,+∞).
故 g(x)=
| f′(x) |
| x |
| a2+a |
| x |
∵g(x)=
| f′(x) |
| x |
∴?x≠0,g(-x)+g(x)=0,即2a+1=0,
∴a=-
| 1 |
| 2 |
(Ⅱ)f'(x)=x2-(2a+1)x+(a2+a)=(x-a)[x-(a+1)],
列表如下:
| x | (-∞,a) | (a,a+1) | (a+1,+∞) |
| f'(x) | + | - | + |
由题设a+1=2,∴a=1;
所以函数的递增区间为(-∞,1),(2,+∞).
点评:本题考查导数的运用:求单调区间和求极值,考查函数的奇偶性及运用,考查求导的运算能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知函数f(x)=
,若存在x1,x2,当0≤x1<4≤x2≤6时,f(x1)=f(x2),则x1•f(x2)的取值范围是( )
|
| A、[0,1) |
| B、[1,4] |
| C、[1,6] |
| D、[0,1]∪[3,8] |
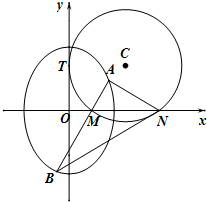 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的左侧),且|MN|=3.
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的左侧),且|MN|=3.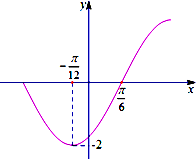
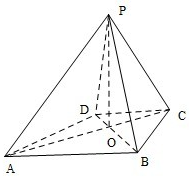 如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=
如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=