题目内容

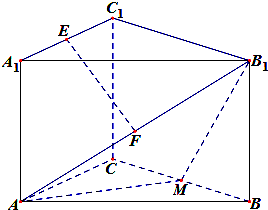在正三棱柱ABC-A1B1C1中，BC=
2
BB1，E、F、M分别为棱A1C1、AB1、BC的中点，
（1）求证：EF∥平面BB1C1C；
（2）求证：EF⊥平面AB1M．
考点：直线与平面垂直的判定,直线与平面平行的判定
专题：空间位置关系与距离
分析：（1）连结A1B，BC1，利用三角形的中位线的性质得到EF∥BC1，利用线面平行的判定定理得证；
（2）首先判断EF⊥B1M，然后利用三棱柱的性质EF⊥AM，结合线面垂直的判定定理得证．
解答： 证明：（1）连结A1B，BC1，
∵E、F分别为棱A1C1、AB1的中点，
∴EF∥BC1，
∵BC1?平面BB1C1C，EF?平面BB1C1C
∴EF∥平面BB1C1C
（2）在矩形BCC1B1中，BC=
2
BB1，
tan(∠CBC1)=
2
2
，tan(∠B1MB)=
2

∴tan∠CBC1•tan∠B1MB=1
∴∠CBC1+∠B1MB=
π
2

∴BC1⊥B1M
∵EF∥BC1
∴EF⊥B1M
在正三棱柱ABC-A1B1C1中，底面ABC⊥平面BB1C1C
∵M为BC的中点
∴AM⊥BC
∵平面ABC∩平面BB1C1C=BC
∴AM⊥平面BB1C1C
∵BC1?平面BB1C1C
∴AM⊥BC1
∵EF∥BC1
∴EF⊥AM
又∵AM∩B1M=M
∴EF⊥平面AB1M．
点评：本题考查了三棱柱中线面平行的判断和线面垂直的判断，关键是结合三棱柱的性质以及线面平行、垂直的判定定理解答．
练习册系列答案
相关题目
设α，β是两个平面，α∩β=b，且直线a∥α，a∥β，那么请画图表示a与b的位置关系．并证明．
化简下列各式：
（1）
a
1
2
-b
1
2
a
1
2
+b
1
2
+
a
1
2
+b
1
2
a
1
2
-b
1
2
；
（2）（a2-2+a-2）÷（a2-a-2）．
若函数y=f（x）对定义域D的每一个x1，都存在唯一的x2∈D，使f（x1）f（x2）=1成立，则称f（x）为“自倒函数”，下列命题正确的是
 
．（把你认为正确自倒函数命题的序号都填上）
（1）f（x）=sinx+
2
（x∈[-
π
2
，
π
2
]）是自倒函数；  
（2）自倒函数f（x）的值域可以是R；
（3）自倒函数f（x）的可以是奇函数；
（4）若y=f（x），y=g（x）都是自倒函数，且定义域相同，则y=f（x）•g（x）是自倒函数．
下列说法不正确的是（　　）
A、命题“对?x∈R，都有x2≥0”的否定为“?x0∈R，使得x02＜0”
B、“a＞b”是“ac2＞bc2”的必要不充分条件
C、“若tanα≠
3
，则α≠
π
3
”是真命题
D、甲、乙两位学生参与数学模拟考试，设命题p是“甲考试及格”，q是“乙考试及格”，则命题“至少有一位学生不及格”可表示为（￢p）∧（￢q）
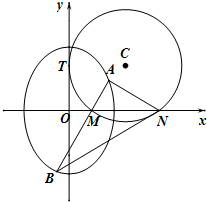如图，圆C与y轴相切于点T（0，2），与x轴正半轴相交于两点M，N（点M在点N的左侧），且|MN|=3．
（Ⅰ）求圆C的方程；
（Ⅱ）过点M任作一条直线与椭圆Γ：
x2
4
+
y2
8
=1相交于两点A、B，连接
AN、BN，求证：∠ANM=∠BNM．
已知函数g（x）=b2lnx-bx-3（b∈R）的极值点为x=1，函数h（x）=ax2+bx+4b-1．
（Ⅰ）求函数g（x）的单调区间，并比较g（x）与g（1）的大小关系；
（Ⅱ）当a=
1
2
时，函数t（x）=ln（1+x2）-h（x）+x+4-k（k∈R），试判断函数t（x）的零点个数；
（Ⅲ）如果函数f（x），f1（x），f2（x）在公共定义域D上，满足f1（x）＜f（x）＜f2（x），那么就称f（x）为f1（x），f2（x）的“伴随函数”，已知函数f1（x）=（a-
1
2
）x2+2ax+（1-a2）lnx，f2（x）=
1
2
x2+2ax，若在区间（1，+∞）上，函数f（x）=g（x）+h（x）是f1（x），f2（x）的“伴随函数”，求a的取值范围．
设非空集合A，若对A中任意两个元素a，b，通过某个法则“•”，使A中有唯一确定的元素c与之对应，则称法则“•”为集合A上的一个代数运算．若A上的代数运算“•”还满足：（1）对?a，b，c∈A，都有（a•b）•c=a•（b•c）；（2）对?a∈A，?e，b∈A，使得e•a=a•e=a，a•b=b•a=e．称A关于法则“•”构成一个群．给出下列命题：
①实数的除法是实数集上的一个代数运算；
②自然数集关于自然数的加法不能构成一个群；
③非零有理数集关于有理数的乘法构成一个群；
④正整数集关于法则a°b=ab构成一个群．
其中正确命题的序号是
 
．（填上所有正确命题的序号）．
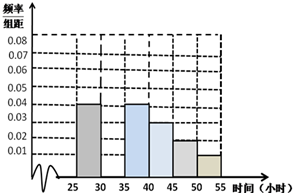教育部，体育总局和共青团中央号召全国各级各类学校要广泛，深入地开展全国亿万大，中学生阳光体育运动，为此，某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计，随机抽取了100名学生作为样本，得到这100名学生在该月参加体育运动总时间的小时数，根据此数据作出了如下的频数和频率的统计表和 频率分布直方图：
（I）求a，p的值，并补全频率分布直方图；
（Ⅱ）根据上述数据和直方图，试估计运动时间在[25，55]小时的学生体育运动的平均时间；
分组运动时间
（小时）		频数频率
1[25，30）200.2
2[30，35） ap
3[35，40）200.2
4[40，45）150.15
5[45，50）100.10
6[50，55]50.05

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网