题目内容
已知矩阵A=
,若矩阵A属于特征值6的一个特征向量为α1=
,属于特征值1的一个特征向量为α2=
.
(1)求矩阵A;
(2)求出直线x+y-1=0在矩阵A对应的变换作用下所得曲线的方程.
|
|
|
(1)求矩阵A;
(2)求出直线x+y-1=0在矩阵A对应的变换作用下所得曲线的方程.
考点:矩阵特征值的定义,几种特殊的矩阵变换
专题:矩阵和变换
分析:本题(1)可以利用矩阵的特征值和特征向量的意义列出相应的方程,解方程得到本题结论;(2)根据矩阵变换下相关点的坐标关系,利用代入法求出曲线的方程,得到本题结论.
解答:
解:(1)∵矩阵A=
,若矩阵A属于特征值6的一个特征向量为α1=
,属于特征值1的一个特征向量为α2=
,
∴
•
=6
,
•
=
,
∴
,
∴
.
∴A=
.
(2)设直线x+y-1=0上一点P(x,y)在矩阵A的作用下得到曲线xy=1上一点P′(x′,y′),
∴
=
,
∴
,即
,
将上式代入x+y-1=0得:x′-
y′-1=0,
∴2x-y-2=0.
∴直线x+y-1=0在矩阵A对应的变换作用下所得曲线的方程为2x-y-2=0.
|
|
|
∴
|
|
|
|
|
|
∴
|
∴
|
∴A=
|
(2)设直线x+y-1=0上一点P(x,y)在矩阵A的作用下得到曲线xy=1上一点P′(x′,y′),
∴
|
|
|
∴
|
|
将上式代入x+y-1=0得:x′-
| 1 |
| 2 |
∴2x-y-2=0.
∴直线x+y-1=0在矩阵A对应的变换作用下所得曲线的方程为2x-y-2=0.
点评:本题考查了矩阵的特征值和特征向量以及矩阵变换下曲线的方程,本题难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
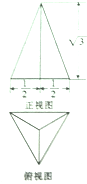
已知三棱锥的底面是正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x)=
,若存在x1,x2,当0≤x1<4≤x2≤6时,f(x1)=f(x2),则x1•f(x2)的取值范围是( )
|
| A、[0,1) |
| B、[1,4] |
| C、[1,6] |
| D、[0,1]∪[3,8] |
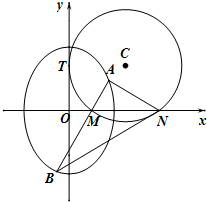 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的左侧),且|MN|=3.
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的左侧),且|MN|=3.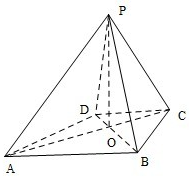 如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=
如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=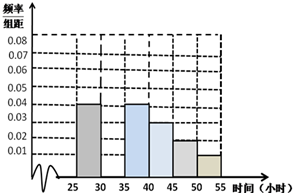 教育部,体育总局和共青团中央号召全国各级各类学校要广泛,深入地开展全国亿万大,中学生阳光体育运动,为此,某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计,随机抽取了100名学生作为样本,得到这100名学生在该月参加体育运动总时间的小时数,根据此数据作出了如下的频数和频率的统计表和 频率分布直方图:
教育部,体育总局和共青团中央号召全国各级各类学校要广泛,深入地开展全国亿万大,中学生阳光体育运动,为此,某校学生会对高二年级2014年9月与10月这两个月内参加体育运动的情况进行统计,随机抽取了100名学生作为样本,得到这100名学生在该月参加体育运动总时间的小时数,根据此数据作出了如下的频数和频率的统计表和 频率分布直方图: