题目内容
如图,在梯形PDCB中,BC=PD,DC∥PB,PB=3DC=3,PD=
,DA⊥PB,将△PAD沿AD折起,使得PA⊥AB,得到四棱锥P-ABCD,点M在棱PB上.
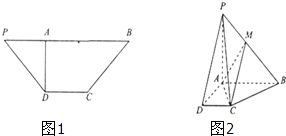
(Ⅰ) 证明:平面PAD⊥平面PCD;
(Ⅱ) 如果AM⊥PB,求二面角C-AM-B的正切值;
(Ⅲ)当PD∥平面AMC时,求三棱锥P-ABC与三棱锥M-ABC的体积之比.
| 2 |

(Ⅰ) 证明:平面PAD⊥平面PCD;
(Ⅱ) 如果AM⊥PB,求二面角C-AM-B的正切值;
(Ⅲ)当PD∥平面AMC时,求三棱锥P-ABC与三棱锥M-ABC的体积之比.
考点:与二面角有关的立体几何综合题,棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由图1中DA⊥PB,可得折叠后DA⊥AB,DA⊥PA,进而DC⊥PA,DC⊥DA,由线面垂直的判定定理得到DC⊥平面PAD,再由面面垂直的判定定理得到平面PAD⊥平面PCD;
(Ⅱ) 以A为坐标原点,建立空间坐标系,分别求出平面ACM和平面ABM的法向量,代入向量夹角公式,可得二面角C-AM-B的余弦值,进而根据同角三角函数关系,可得二面角C-AM-B的正切值;
(Ⅲ)当PD∥平面AMC时,根据平行线分线段成比例定理和相似三角形的性质,可得
=
,即三棱锥P-ABC与三棱锥M-ABC的高之比为
,即三棱锥P-ABC与三棱锥M-ABC的体积之比为
.
(Ⅱ) 以A为坐标原点,建立空间坐标系,分别求出平面ACM和平面ABM的法向量,代入向量夹角公式,可得二面角C-AM-B的余弦值,进而根据同角三角函数关系,可得二面角C-AM-B的正切值;
(Ⅲ)当PD∥平面AMC时,根据平行线分线段成比例定理和相似三角形的性质,可得
| PM |
| MB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
证明:(Ⅰ)因为在图a的等腰梯形PDCB中,DA⊥PB,
所以在四棱锥P-ABCD中,DA⊥AB,DA⊥PA.
又PA⊥AB,且DC∥AB,所以DC⊥PA,DC⊥DA,
而DA?平面PAD,PA?平面PAD,PA∩DA=A,
所以DC⊥平面PAD.
因为DC?平面PCD,
所以平面PAD⊥平面PCD.
(II)以A为坐标原点,建立空间坐标系,如下图所示:
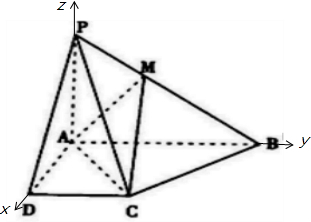
∵PB=3DC=3,PD=
,故AD=1,AB=2,AP=1,
故PB=
=
,
当AM⊥PB时,由射影定理可得PM=
PB,
∴A(0,0,0),B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),
∴
=(1,1,0),
=(0,2,0),
=(0,0,1),
∴
=
+
=(0,
,
),
设平面ACM的一个法向量为
=(x,y,z),
由
得:
,
即
,
令x=2,则
=(2,-2,1),
由
=(1,0,0)为平面MAB的法向量,
故二面角C-AM-B的平面角θ满足:
cosθ=
=
,
故sinθ=
=
,
故tanθ=
=
;
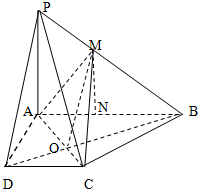
(III)在梯形ABCD中,连接AC、BD交于点O,连接OM.
∵PD∥平面AMC,PD?平面PBD,平面PBD∩平面AMC=MO,
∴PD∥MO
∴
=
,
∵△AOB∽△DOC,
∴
=
=
,
即
=
,
即三棱锥P-ABC与三棱锥M-ABC的高之比为
,
即三棱锥P-ABC与三棱锥M-ABC的体积之比为
.
所以在四棱锥P-ABCD中,DA⊥AB,DA⊥PA.
又PA⊥AB,且DC∥AB,所以DC⊥PA,DC⊥DA,
而DA?平面PAD,PA?平面PAD,PA∩DA=A,
所以DC⊥平面PAD.
因为DC?平面PCD,
所以平面PAD⊥平面PCD.
(II)以A为坐标原点,建立空间坐标系,如下图所示:

∵PB=3DC=3,PD=
| 2 |
故PB=
| 22+12 |
| 5 |
当AM⊥PB时,由射影定理可得PM=
| 1 |
| 5 |
∴A(0,0,0),B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),
∴
| AC |
| AB |
| AP |
∴
| AM |
| 4 |
| 5 |
| AP |
| 1 |
| 5 |
| AB |
| 2 |
| 5 |
| 4 |
| 5 |
设平面ACM的一个法向量为
| m |
由
|
|
即
|
令x=2,则
| m |
由
| AD |
故二面角C-AM-B的平面角θ满足:
cosθ=
|
| ||||
|
|
| 2 |
| 3 |
故sinθ=
| 1-cos2θ |
| ||
| 3 |
故tanθ=
| sinθ |
| cosθ |
| ||
| 2 |
(III)在梯形ABCD中,连接AC、BD交于点O,连接OM.
∵PD∥平面AMC,PD?平面PBD,平面PBD∩平面AMC=MO,
∴PD∥MO

∴
| DO |
| OB |
| PM |
| MB |
∵△AOB∽△DOC,
∴
| DO |
| OB |
| CD |
| AB |
| 1 |
| 2 |
即
| PM |
| MB |
| 1 |
| 2 |
即三棱锥P-ABC与三棱锥M-ABC的高之比为
| 1 |
| 2 |
即三棱锥P-ABC与三棱锥M-ABC的体积之比为
| 1 |
| 2 |
点评:本题考查的知识点是与二面角有关的立体几何综合体,棱锥的体积,平面与平面垂直的判定定理,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
复数z1=1+bi,z2=-2+i,若
的对应点位于直线x+y=0上,则实数b的值为( )
| z1 |
| z2 |
| A、-3 | ||
| B、3 | ||
C、-
| ||
D、
|
已知sinα=
,则cos(π+2α)的值为( )
| 1 |
| 3 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
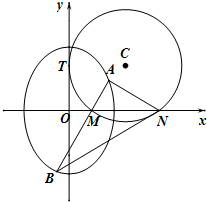 如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的左侧),且|MN|=3.
如图,圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的左侧),且|MN|=3.