题目内容
对任意实数x，（a2-1）x2+（a-1）x-1＜0都成立，则a的取值范围是 ．
考点：二次函数的性质
专题：计算题,函数的性质及应用
分析：讨论当a2-1=0，即a=±1，分别考虑a=1，a=-1，是否恒成立，再讨论当a2-1≠0时，由条件得，a2-1＜0且（a-1）2+4（a2-1）＜0，解出即可得到．
解答：
解：当a2-1=0，即a=±1，当a=1时，-1＜0恒成立，当a=-1时，-2x-1＜0不恒成立；
当a2-1≠0时，由条件得，a2-1＜0且（a-1）2+4（a2-1）＜0，
解得-1＜a＜1且-
＜a＜1，则有-
＜a＜1．
综上，可得a的取值范围是：（-
，1]．
故答案为：（-
，1]．
当a2-1≠0时，由条件得，a2-1＜0且（a-1）2+4（a2-1）＜0，
解得-1＜a＜1且-
| 3 |
| 5 |
| 3 |
| 5 |
综上，可得a的取值范围是：（-
| 3 |
| 5 |
故答案为：（-
| 3 |
| 5 |
点评：本题考查含参的二次不等式的恒成立问题，注意讨论二次项的系数是否为0，以及结合图象的开口方向和判别式小于0，同时考查二次不等式的解法，属于中档题．
练习册系列答案
相关题目
若在甲袋内装有8个白球，4个红球，在乙袋内装有6个白球，6个红球，今从两袋里面各任意取出1个球，设取去的白球的个数为ξ，则下列概率中等于
的是（ ）
| ||||||||
|
| A、P（ξ=0） |
| B、P（ξ≤2） |
| C、P（ξ=1） |
| D、P（ξ=2） |
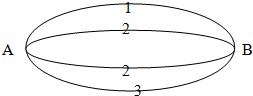如图A、B两点之间有4条网线并联，他们能通过的最大信息量分别为1、2、2、3，现从中任取三条网线且使每条网线通过最大信息量；抛物线x2+y=0的焦点坐标是（ ）
A、（0，-
| ||
B、（0，
| ||
C、（
| ||
D、（-
|