题目内容
设函数f(x)=x3+ax2-a2x+1,g(x)=ax2-2x+1,其中实数a≠0.
(Ⅰ)若a>0,求函数f(x)的单调区间;
(Ⅱ)若f(x)与g(x)在区间(a,a+2)内均为增函数,求实数a的取值范围;
(Ⅲ)当函数y=f(x)与y=g(x)的图象只有一个公共点且g(x)存在最小值时,记g(x)的最小值为h(a),求h(a)的值域.
(Ⅰ)若a>0,求函数f(x)的单调区间;
(Ⅱ)若f(x)与g(x)在区间(a,a+2)内均为增函数,求实数a的取值范围;
(Ⅲ)当函数y=f(x)与y=g(x)的图象只有一个公共点且g(x)存在最小值时,记g(x)的最小值为h(a),求h(a)的值域.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由f'(x)=3x2+2ax-a2=(3x-a)(x+a),a>0,由f′(x)>0,得x<-a,x>
.由此能求出f(x)的单调区间.
(Ⅱ)g(x)对称轴为x=
,当a>0时,a≥
且a≥
;当a<0时,a+2≤
且a+2≤
.由此能求出实数a的取值范围.
(Ⅲ)由已知条件知(a2-2))=0只有一个实根,二次函数y=g(x)有最小值,由此能求出h(a)的值域.
| a |
| 3 |
(Ⅱ)g(x)对称轴为x=
| 1 |
| a |
| a |
| 3 |
| 1 |
| a |
| a |
| 3 |
| 1 |
| a |
(Ⅲ)由已知条件知(a2-2))=0只有一个实根,二次函数y=g(x)有最小值,由此能求出h(a)的值域.
解答:
解:(Ⅰ)∵f(x)=x3+ax2-a2x+1,
∴f'(x)=3x2+2ax-a2=(3x-a)(x+a),
∵a>0,∴由f′(x)>0,得x<-a,x>
.
∴f(x)的递减区间为(-a,
);
递增区间为(-∞,-a),(
,+∞)…(4分)
(Ⅱ)∵g(x)=ax2-2x+1=a(x-
)2-
+1,
∴对称轴为x=
,
当a>0时,由(Ⅰ)知f(x)的递增区间为(-∞,-a),(
,+∞),
∵g(x)在(
,+∞)递增,
依题意(a,a+2)⊆(
,+∞),
且(a,a+2)⊆(
,+∞),∴a≥
且a≥
,解得a≥1.…(6分)
当a<0时,f(x)的递增区间为(-∞,
),(-a,+∞),
g(x)在(-∞,
)递增,
依题意(a,a+2)⊆(-∞,
)且(a,a+2)⊆(-∞,
),
∴a+2≤
且a+2≤
,解得a≤-3.
∴实数a的取值范围为a≤-3或a≥1.(8分)
(Ⅲ)由函数y=f(x),y=g(x)关于x方程:x3+ax2-a2x+1=ax2-2x+1,
即(a2-2))=0只有一个实根,
∴a2-2≤0,解得-
≤a≤
.
二次函数y=g(x)存在最小值,
∴a>0,∴0<a≤
…(10分)
∵g(x)=ax2-2x+1=a(x-
)2-
+1,
∴h(a)=1-
,∴h(a)的值域为(-∞,1-
].…(12分)
∴f'(x)=3x2+2ax-a2=(3x-a)(x+a),
∵a>0,∴由f′(x)>0,得x<-a,x>
| a |
| 3 |
∴f(x)的递减区间为(-a,
| a |
| 3 |
递增区间为(-∞,-a),(
| a |
| 3 |
(Ⅱ)∵g(x)=ax2-2x+1=a(x-
| 1 |
| a |
| 1 |
| a |
∴对称轴为x=
| 1 |
| a |
当a>0时,由(Ⅰ)知f(x)的递增区间为(-∞,-a),(
| a |
| 3 |
∵g(x)在(
| 1 |
| a |
依题意(a,a+2)⊆(
| a |
| 3 |
且(a,a+2)⊆(
| 1 |
| a |
| a |
| 3 |
| 1 |
| a |
当a<0时,f(x)的递增区间为(-∞,
| a |
| 3 |
g(x)在(-∞,
| 1 |
| a |
依题意(a,a+2)⊆(-∞,
| a |
| 3 |
| 1 |
| a |
∴a+2≤
| a |
| 3 |
| 1 |
| a |
∴实数a的取值范围为a≤-3或a≥1.(8分)
(Ⅲ)由函数y=f(x),y=g(x)关于x方程:x3+ax2-a2x+1=ax2-2x+1,
即(a2-2))=0只有一个实根,
∴a2-2≤0,解得-
| 2 |
| 2 |
二次函数y=g(x)存在最小值,
∴a>0,∴0<a≤
| 2 |
∵g(x)=ax2-2x+1=a(x-
| 1 |
| a |
| 1 |
| a |
∴h(a)=1-
| 1 |
| a |
| ||
| 2 |
点评:本题考查函数的单调区间的求法,考查实数的取值范围的求法,考查函数的值域的求法,解题时要认真审题,注意导数的性质的灵活运用.

练习册系列答案
相关题目
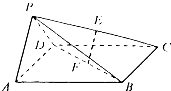 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,PA⊥PD,E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,PA⊥PD,E、F分别为PC、BD的中点.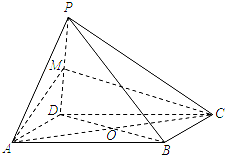 如图,四棱锥P-ABCD中,O为菱形ABCD对角线的交点,M为棱PD的中点,MA=MC.
如图,四棱锥P-ABCD中,O为菱形ABCD对角线的交点,M为棱PD的中点,MA=MC.
 如图,已知点P在正方体ABCD-A1B1C1D1的对角线BD1上,∠PDA=60°.
如图,已知点P在正方体ABCD-A1B1C1D1的对角线BD1上,∠PDA=60°.