题目内容
棱长均为3的三棱锥S-ABC，若空间一点P满足
=x
+y
+z
(x+y+z=1)，则|
|的最小值为 ．
| SP |
| SA |
| SB |
| SC |
| SP |
考点：棱锥的结构特征
专题：平面向量及应用,空间位置关系与距离
分析：欲求|
|的最小值，将其平方，先利用空间向量的数量积运算出|
|2，即
2的值，再将题中条件：x+y+z=1代入运算，最后利用基本不等式即可求得最小值．
| SP |
| SP |
| SP |
解答：
解：∵空间一点P满足
=x
+y
+z
(x+y+z=1)，
∵x+y+z=1，
∴（x+y+z）2=x2+y2+z2+2xy+2xz+2yz=1，
又x2+y2+z2≥xy+xz+yz，
∴xy+xz+yz≤
，
∴x2+y2+z2+xy+xz+yz
=1-（xy+xz+yz）≥
，
∴
2=（x
+y
+z
）2
=9（x2+y2+z2）+（2xy
•
+2xz
•
+2yz
•
）=9（x2+y2+z2+xy+xz+yz）≥6，
则|
|的最小值为
．
故答案：
．
| SP |
| SA |
| SB |
| SC |
∵x+y+z=1，
∴（x+y+z）2=x2+y2+z2+2xy+2xz+2yz=1，
又x2+y2+z2≥xy+xz+yz，
∴xy+xz+yz≤
| 1 |
| 3 |
∴x2+y2+z2+xy+xz+yz
=1-（xy+xz+yz）≥
| 2 |
| 3 |
∴
| SP |
| SA |
| SB |
| SC |
=9（x2+y2+z2）+（2xy
| SA |
| SB |
| SA |
| SC |
| SC |
| SB |
则|
| SP |
| 6 |
故答案：
| 6 |
点评：本题主要考查了空间向量的数量积运算，以及基本不等式等知识，解答的关键是适当变形成可以利用基本不等式的形式．属于基础题．
练习册系列答案
相关题目
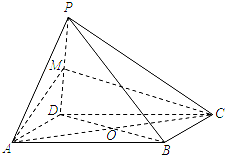如图，四棱锥P-ABCD中，O为菱形ABCD对角线的交点，M为棱PD的中点，MA=MC．
如图，已知点P在正方体ABCD-A1B1C1D1的对角线BD1上，∠PDA=60°．