题目内容
比较下列各组数的大小:
(1)2.8-
,0.8-
;
(2)(
)
,1.5-0.2,1.30.7.
(1)2.8-
| 3 |
| 2 |
| 1 |
| 2 |
(2)(
| 2 |
| 3 |
| 1 |
| 3 |
考点:不等式比较大小
专题:函数的性质及应用
分析:(1)利用指数函数的单调性即可得出;
(2)利用指数函数的单调性即可得出,注意与1的大小比较.
(2)利用指数函数的单调性即可得出,注意与1的大小比较.
解答:
解:(1)∵2.8-
<1<0.8-
,
∴2.8-
<0.8-
;
(2)∵1.5-0.2=(
)-1×(-.02)=(
)
>(
)
,且(
)
<1,
1.30.7>1,
∴1.30.7>1.5-0.2>(
)
.
| 3 |
| 2 |
| 1 |
| 2 |
∴2.8-
| 3 |
| 2 |
| 1 |
| 2 |
(2)∵1.5-0.2=(
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 5 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 5 |
1.30.7>1,
∴1.30.7>1.5-0.2>(
| 2 |
| 3 |
| 1 |
| 3 |
点评:本题考查了指数函数的单调性,同时注意与1的大小比较,考查了推理能力,属于基础题.

练习册系列答案
相关题目
已知sin(α-2π)=2sin(
π+α),且α≠kπ+
(k∈Z),则
的值为( )
| 3 |
| 2 |
| π |
| 2 |
| 3sin2α-sin2α |
| 3+cos2α |
A、
| ||
B、
| ||
C、
| ||
D、
|
命题:?x,y∈R,如果xy=0,则x=0.它的否命题为( )
| A、?x,y∈R,如果xy≠0,则x≠0 |
| B、?x,y∈R,如果xy=0,则x≠0 |
| C、?x,y∈R,如果xy≠0,则x≠0 |
| D、?x,y∈R,如果xy=0,则x≠0 |
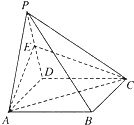 如图,已知正三角形PAD,正方形ABCD,平面PAD⊥平面ABCD,E为PD的中点.
如图,已知正三角形PAD,正方形ABCD,平面PAD⊥平面ABCD,E为PD的中点.