题目内容
函数y=6x-
的最大值是 .
| 1-2x |
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:根据解析式设t=
且t≥0,在求出x代入解析式化简,利用二次函数的性质求出函数的最大值.
| 1-2x |
解答:
解:设t=
,则t≥0,且x=
,
原函数化为:y=3(1-t2)-t=-3t2-t+3,
对称轴方程t=-
=-
,所以此函数在区间[0,+∞)上单调递减,
所以函数的最大值是3,
故答案为:3.
| 1-2x |
| 1-t2 |
| 2 |
原函数化为:y=3(1-t2)-t=-3t2-t+3,
对称轴方程t=-
| -1 |
| 2×(-3) |
| 1 |
| 6 |
所以函数的最大值是3,
故答案为:3.
点评:本题考查利用换元法求函数的最值,以及二次函数的性质,注意换元后应求出它的范围.

练习册系列答案
相关题目
函数f(x)=(x2-2014x-2015),ln(x-2011)的零点有( )
| A、3个 | B、2个 | C、1个 | D、0个 |
定义在R上的函数满足f(x+y)=f(x)+f(y),且在区间(0,+∞)上单调递增,若实数a满足2f(log2a)+f(log
a)≤f(1),则a的取值范围是( )
| 1 |
| 2 |
| A、[1,2] | ||
B、(0,
| ||
| C、(0,2] | ||
| D、(-∞,2] |
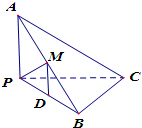 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.