题目内容
已知sin(α-2π)=2sin(
π+α),且α≠kπ+
(k∈Z),则
的值为( )
| 3 |
| 2 |
| π |
| 2 |
| 3sin2α-sin2α |
| 3+cos2α |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:直接利用诱导公式化简已知条件,然后化简所求表达式的值,求解即可.
解答:
解:sin(α-2π)=2sin(
π+α),
∴sinα=-2cosα,
=
=
=
.
故选:D.
| 3 |
| 2 |
∴sinα=-2cosα,
| 3sin2α-sin2α |
| 3+cos2α |
| 3sin2α-2sinαcosα |
| 4cos2α+2sin2α |
| 12cos2α+4cosαcosα |
| 4cos2α+8cos2α |
| 4 |
| 3 |
故选:D.
点评:本题考查诱导公式的应用,萨迦寺的化简求值,开采技术能力.

练习册系列答案
相关题目
定义在R上的函数满足f(x+y)=f(x)+f(y),且在区间(0,+∞)上单调递增,若实数a满足2f(log2a)+f(log
a)≤f(1),则a的取值范围是( )
| 1 |
| 2 |
| A、[1,2] | ||
B、(0,
| ||
| C、(0,2] | ||
| D、(-∞,2] |
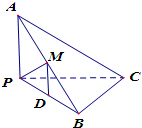 如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.
如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形.