题目内容
设点P是以F1，F2为左、右焦点的双曲线
-
=1（a＞0，b＞0）左支上一点，且满足
•
=0，tan∠PF2F1=
，则此双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由
•
=0，tan∠PF2F1=
，可得PF1⊥PF2，且|PF1|：|PF2|=2：3，结合|PF2|-|PF1|=2a，可得|PF2|=6a，|PF1|=4a，在RT△PF1F2中，利用余弦定理，即可求出双曲线的离心率．
| PF1 |
| PF2 |
| 2 |
| 3 |
解答：
解：∵
•
=0，tan∠PF2F1=
，
∴PF1⊥PF2，且|PF1|：|PF2|=2：3，
∵|PF2|-|PF1|=2a，
∴|PF2|=6a，|PF1|=4a，
在RT△PF1F2中，|F1F2|2=|PF1|2+|PF2|2，
∴4c2=36a2+16a2，解得e=
故选：D．
| PF1 |
| PF2 |
| 2 |
| 3 |
∴PF1⊥PF2，且|PF1|：|PF2|=2：3，
∵|PF2|-|PF1|=2a，
∴|PF2|=6a，|PF1|=4a，
在RT△PF1F2中，|F1F2|2=|PF1|2+|PF2|2，
∴4c2=36a2+16a2，解得e=
| 13 |
故选：D．
点评：本题主要考察了双曲线的离心率的求解，属中档题，解题的关键是抓住要求离心率即根据题中条件建立关于a，b，c的关系式．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
确定结论“X与Y有关系”的可信度为99.5%时，则随即变量k2的观测值k必须（ ）
| A、小于7.879 |
| B、大于10.828 |
| C、小于6.635 |
| D、大于2.706 |
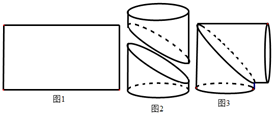工人师傅在如图1的一块矩形铁皮上画一条曲线，沿曲线剪开，将所得到的两部分卷成圆柱状，如图2，然后将其对接，可做成一个直角的“拐脖”，如图3．工人师傅所画的曲线是（ ）| A、一段圆弧 |
| B、一段抛物线 |
| C、一段双曲线 |
| D、一段正弦曲线 |
如果椭圆
+
=1上一点p到焦点F1的距离等于3，那么点p到另一个焦点F2的距离是（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| A、4 | B、3 | C、2 | D、1 |
已知△ABC中，点D在BC边上，且
=4
=r
+s
，则3r+s=（ ）
| CD |
| DB |
| AB |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
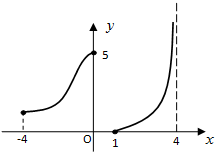如图所示是函数y=f（x）的图象，图中曲线与直线无限接近但是永不相交，则以下描述正确的是（ ）| A、函数f（x）的定义域为[-4，4） |
| B、函数f（x）的值域为[0，5] |
| C、此函数在定义域中不单调 |
| D、对于任意的y∈[0，+∞），都有唯一的自变量x与之对应 |
在△ABC中，A，B，C所对的边分别是a，b，c，满足3a2+3b2=c2+4ab，现设f（x）=tanx，则（ ）
| A、f（sinA）≤f（cosB） |
| B、f（sinA）≥f（cosB） |
| C、f（sinA）≤f（sinB） |
| D、f（cosA）≤f（cosB） |