题目内容
已知函数f(x)=ex-ax-1(a∈R).
(Ⅰ)当a>0时,求函数f(x)的单调区间;
(Ⅱ)函数F(x)=f(x)-xlnx在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
(Ⅲ)若f(x)≥0对任意x≥0恒成立,求a的取值范围.
(Ⅰ)当a>0时,求函数f(x)的单调区间;
(Ⅱ)函数F(x)=f(x)-xlnx在定义域内是否存在零点?若存在,请指出有几个零点;若不存在,请说明理由;
(Ⅲ)若f(x)≥0对任意x≥0恒成立,求a的取值范围.
考点:利用导数研究函数的单调性,函数零点的判定定理
专题:导数的综合应用
分析:(Ⅰ)直接对f(x)求导,当a>0时,f′(x)=ex-a的正负即可确定函数f(x)单调区间;
(Ⅱ)对F(x)=f(x)-xlnx进行化简,构造函数h(x)=
-lnx(x>0),研究函数h(x)的单调性和最小值,即可确定F(x)=f(x)-xlnx在定义域内是否存在零点;
(Ⅲ)求f(x)的导数,利用导数研究函数f(x)在[0,+∞)的单调性,然后讨论a的取值,从而确定f(x)的最值,即可确定实数a的取值范围.
(Ⅱ)对F(x)=f(x)-xlnx进行化简,构造函数h(x)=
| ex-1 |
| x |
(Ⅲ)求f(x)的导数,利用导数研究函数f(x)在[0,+∞)的单调性,然后讨论a的取值,从而确定f(x)的最值,即可确定实数a的取值范围.
解答:
解:(Ⅰ)由f(x)=ex-ax-1,则f′(x)=ex-a.
由f′(x)>0,得x>lna;由f′(x)<0,得x<lna,
所以函数f(x)的单调增区间为(lna,+∞),单调减区间为(-∞,lna);
(Ⅱ)函数F(x)=f(x)-xlnx的定义域为(0,+∞),
由F(x)=0,得a=
-lnx(x>0)
令h(x)=
-lnx(x>0),则h′(x)=
,
由于x>0,ex-1>0,可知当x>1,h′(x)>0;当0<x<1时,h′(x)<0,
故函数h(x)在(0,1)上单调递减,在(1,+∞)上单调递增,故h(x)≥h(1)=e-1.
又由(Ⅰ)知当a=1时,对?x>0,有f(x)>f(lna)=0,即ex-1>x?
>1,
当a>e-1时,函数F(x)有两个不同的零点;
当a=e-1时,函数F(x)有且仅有一个零点;
当a<e-1时,函数F(x)没有零点.
(Ⅲ)由f(x)=ex-ax-1,则f′(x)=ex-a.
①当a≤1时,对?x≥0,有f′(x)>0,所以函数f(x)在区间(0,+∞)上单调递增,
又f(0)=0,即f(x)≥f(0)=0对?x≥0恒成立.
②当a>1时,由(Ⅰ),f(x)单调递增区间为(lna,+∞),单调递减区间为(-∞,lna),
若f(x)≥0对任意x≥0恒成立,只需f(x)min=f(lna)=a-alna-1≥0,
令g(a)=a-alna-1(a>1),g′(a)=1-lna-1=-lna<0,
即g(a)在区间(1,+∞)上单调递减,又g(1)=0,故g(a)<0在(1,+∞)上恒成立,
故当a>1时,满足a-alna-1≥0的a不存在.
综上所述,a的取值范围是(-∞,1].
由f′(x)>0,得x>lna;由f′(x)<0,得x<lna,
所以函数f(x)的单调增区间为(lna,+∞),单调减区间为(-∞,lna);
(Ⅱ)函数F(x)=f(x)-xlnx的定义域为(0,+∞),
由F(x)=0,得a=
| ex-1 |
| x |
令h(x)=
| ex-1 |
| x |
| (ex-1)(x-1) |
| x2 |
由于x>0,ex-1>0,可知当x>1,h′(x)>0;当0<x<1时,h′(x)<0,
故函数h(x)在(0,1)上单调递减,在(1,+∞)上单调递增,故h(x)≥h(1)=e-1.
又由(Ⅰ)知当a=1时,对?x>0,有f(x)>f(lna)=0,即ex-1>x?
| ex-1 |
| x |
当a>e-1时,函数F(x)有两个不同的零点;
当a=e-1时,函数F(x)有且仅有一个零点;
当a<e-1时,函数F(x)没有零点.
(Ⅲ)由f(x)=ex-ax-1,则f′(x)=ex-a.
①当a≤1时,对?x≥0,有f′(x)>0,所以函数f(x)在区间(0,+∞)上单调递增,
又f(0)=0,即f(x)≥f(0)=0对?x≥0恒成立.
②当a>1时,由(Ⅰ),f(x)单调递增区间为(lna,+∞),单调递减区间为(-∞,lna),
若f(x)≥0对任意x≥0恒成立,只需f(x)min=f(lna)=a-alna-1≥0,
令g(a)=a-alna-1(a>1),g′(a)=1-lna-1=-lna<0,
即g(a)在区间(1,+∞)上单调递减,又g(1)=0,故g(a)<0在(1,+∞)上恒成立,
故当a>1时,满足a-alna-1≥0的a不存在.
综上所述,a的取值范围是(-∞,1].
点评:本题以函数为载体,主要考查导数的几何意义,考查导数在研究函数的单调性和最值中的应用,考查恒成立问题的解决方法,属于难题.

练习册系列答案
相关题目
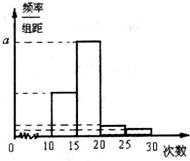 对山东省实验中学高三年级学生参加社区服务次数进行统计,随机抽取m名学生作样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图:
对山东省实验中学高三年级学生参加社区服务次数进行统计,随机抽取m名学生作样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图如图: