Question

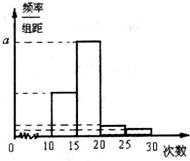对山东省实验中学高三年级学生参加社区服务次数进行统计，随机抽取m名学生作样本，得到这M名学生参加社区服务的次数，根据此数据作出了频数与频率的统计表和频率分布直方图如图：
（Ⅰ）求出表中m，p及图中a的值；
（Ⅱ）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求两人来自同一小组的概率．

分组	频数	频率
[10，15）	10	0.25
[15，20）	24	0.6
[20，25）	m	p
[25，30）	2	0.05
合计	m	1

Answer 1

考点：古典概型及其概率计算公式,频率分布直方图

专题：概率与统计

分析：（Ⅰ）根据频率分布表中的数据可计算总人数M的值，然后利用频率之和为1，可计算p的值；
（Ⅱ）计算出参加社区服务的次数不少于20次的人数，列举任选2人的所有基本事件，找出两人来自同一小组的基本事件个数，利用公式计算即可．

解答： 解：（Ⅰ）由频率分布表知，
[10，15）内的频数为10，频率为0.25，
∵

10

M

=0.25，
∴M=40，
p=1-0.25-0.6-0.05=0.1．
（Ⅱ）∵m=40-10-24-2=4，
∴社区服务的次数不小于20次的学生共有，m+2=6，
[20，25）小组由4人，设为A，B，C，D，
[25，30）小组由2人，设为E，F，
任选2人的基本事件有，
AB，AC，AD，AE，AF，
BC，BD，BE，BF，
CD，CE，CF，
DE，DF，
EF，
共15种，
来自同一组的有AB，AC，AD，BC，BD，CD，EF，共7种，
∴两人来自同一小组的概率为

7

15

．

点评：本题考查频率分布直方图和频率分布表的应用，以及古典概型概率的计算．属于中档题．