题目内容
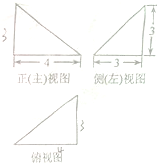
某四面体的三视图如图所示,则该四面体的表面积是( )

| A、21 | B、27 | C、54 | D、60 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知的三视图可得:该几何体是一个以俯视图为底面的三棱锥,分别求出各个面的面积相加可得答案.
解答:
解:根据几何体的三视图知,
该几何体是三棱锥,如图所示;
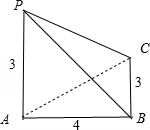
且底面△ABC为俯视图中的直角三角形,∠ABC=90°,
其中AB=4,BC=3,
∴AC=5,
PA⊥底面ABC,且PA=3,
∴∠PAB=∠PAC=90°,CB⊥PB;
∴S△ABC=
AB•BC=
×4×3=6,
S△PAB=
PA•AB=
×3×4=6,
S△PAC=
PA•AC=
×3×5=
,
S△PBC=
PB•BC=
×5×3=
;
∴三棱锥P-ABC的表面积为
S=S△ABC+S△PAB+S△PAC+S△PBC=6+6+
+
=27.
故选:B.
该几何体是三棱锥,如图所示;

且底面△ABC为俯视图中的直角三角形,∠ABC=90°,
其中AB=4,BC=3,
∴AC=5,
PA⊥底面ABC,且PA=3,
∴∠PAB=∠PAC=90°,CB⊥PB;
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
S△PAB=
| 1 |
| 2 |
| 1 |
| 2 |
S△PAC=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
∴三棱锥P-ABC的表面积为
S=S△ABC+S△PAB+S△PAC+S△PBC=6+6+
| 15 |
| 2 |
| 15 |
| 2 |
故选:B.
点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
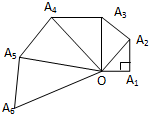 如图OA1=1,直角三角形OAnAn+1(n=1,2,3…)的直角边AnAn+1=
如图OA1=1,直角三角形OAnAn+1(n=1,2,3…)的直角边AnAn+1=| n |
A、an=
| ||||
B、an=
| ||||
C、an=
| ||||
D、an=
|
已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是( )
| A、AB∥m | B、AC⊥m |
| C、AC⊥β | D、AB∥β |
已知正切函数y=tanx的图象关于点M(θ,0)对称,则cosθ=( )
| A、-1或0 | B、1或0 |
| C、-1或0或1 | D、1或-1 |
 以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.
以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.