题目内容

已知正切函数y=tanx的图象关于点M（θ，0）对称，则cosθ=（　　）
A、-1或0B、1或0
C、-1或0或1D、1或-1
考点：正切函数的图象
专题：计算题,三角函数的求值
分析：由题意可得，（θ，0）是正切函数y=tanx的图象的对称中心，故 θ=
kπ
2
，k∈z，由此求得cosθ的值．
解答： 解：∵正切函数y=tanx的图象关于点（θ，0）对称，∴（θ，0）是正切函数y=tanx的图象的对称中心，
∴θ=
kπ
2
，k∈z．
故cosθ=-1，0 或1，
故选：C．
点评：本题主要考查正切函数的对称中心的坐标，属于基础题．
练习册系列答案
相关题目
某四面体的三视图如图所示，则该四面体的表面积是（　　）
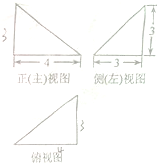
A、21B、27C、54D、60
若从总体中随机抽取的样本为-1，3，-1，1，1，3，2，2，0，0，则该总体的标准差的点估计值是
 
．
f（x）是定义在R上周期为2的函数，在区间[-1，1]时，有f（x）=
ax+1，-1≤x＜0
bx+2
x+1
，0≤x≤1
，其中a，b∈R，若f(
1
2
)=f(
3
2
)，则a+3b的值为
 
．
已知i为虚数单位，则复数z=
2-3i
1+i
对应的点位于（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限
1400°=
 
弧度．
已知△ABC中，acosC+
3
asinC-b-c=0，求∠A大小．
三角形ABC中，角A、B、C所对边分别为a，b，c，且
m
=（
cosB
，
2
），
n
=（sinB，
3
），满足
m
∥
n

（1）若cosA=
1
3
，求sinC的值；
（2）若b=
7
，sinA=3sinC，求三角形ABC的面积．
设A1，A2，…，An是平面上的n个不同的点，则满足
MA1
+
MA2
+…+
MAn
=
0
的点M的个数为（　　）
A、0B、1C、2D、3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网