题目内容
 以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.
以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.(Ⅰ)若甲、乙两个小组的数学平均成绩相同,求a的值;
(Ⅱ)求乙组平均成绩超过甲组平均成绩的概率.
考点:列举法计算基本事件数及事件发生的概率,茎叶图
专题:概率与统计
分析:(Ⅰ)直接由甲、乙两个小组的数学平均成绩相等列式求解a的值;
(Ⅱ)由(Ⅰ)中求得的结果可得,当a=2,…,9时,乙组平均成绩超过甲组平均成绩,然后由古典概率模型概率计算公式求概率;
(Ⅱ)由(Ⅰ)中求得的结果可得,当a=2,…,9时,乙组平均成绩超过甲组平均成绩,然后由古典概率模型概率计算公式求概率;
解答:
解:(Ⅰ)依题意,得
(88+92+92)=
[90+91+(90+a)],
解得 a=1;
(Ⅱ)设“乙组平均成绩超过甲组平均成绩”为事件A,依题意 a=0,1,2,…,9,共有10种可能
由(Ⅰ)可知,当a=1时甲、乙两个小组的数学平均成绩相同,
所以当a=2,3,4,…,9时,乙组平均成绩超过甲组平均成绩,共有8种可能
所以乙组平均成绩超过甲组平均成绩的概率P(A)=
=
| 1 |
| 3 |
| 1 |
| 3 |
解得 a=1;
(Ⅱ)设“乙组平均成绩超过甲组平均成绩”为事件A,依题意 a=0,1,2,…,9,共有10种可能
由(Ⅰ)可知,当a=1时甲、乙两个小组的数学平均成绩相同,
所以当a=2,3,4,…,9时,乙组平均成绩超过甲组平均成绩,共有8种可能
所以乙组平均成绩超过甲组平均成绩的概率P(A)=
| 8 |
| 10 |
| 4 |
| 5 |
点评:本题考查了茎叶图,考查了等可能事件的概率及古典概型概率计算公式,是基础的计算题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
设D是函数y=f(x)定义域内的一个区间,若存在x0∈D,使f(x0)=-x0,则称x0是f(x)的一个“次不动点”,也称f(x)在区间D上存在次不动点.若函数f(x)=ax2-3x-a+
在区间[1,4]上存在次不动点,则实数a的取值范围是( )
| 5 |
| 2 |
| A、(-∞,0) | ||
B、(0,
| ||
C、[
| ||
D、(-∞,
|
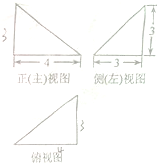
某四面体的三视图如图所示,则该四面体的表面积是( )

| A、21 | B、27 | C、54 | D、60 |
