题目内容

在△ABC中，
BC
=
a
，
CA
=
b
，
AB
=
c
，当（
a
•
b
）：（
c
•
b
）（
a
•
c
）=2：1：3时，求△ABC的三个内角（结果精确到1°）
考点：三角形中的几何计算
专题：计算题,解三角形,平面向量及应用
分析：由题意化简
c
•
b
=bccos（π-A）=-bccosA，
a
•
b
=-abcosC，
a
•
c
=-accosB；从而可得
bccosA
1
=
abcosC
2
=
accosB
3
；再由余弦定理化简得
b2+c2-a2
2
=
a2+b2-c2
4
=
c2+a2-b2
6
=k，从而得到
a2=5k
c2=4k
b2=3k
，再由余弦定理求角．
解答： 解：∵
c
•
b
=bccos（π-A）=-bccosA，
a
•
b
=-abcosC，
a
•
c
=-accosB；
∴
bccosA
1
=
abcosC
2
=
accosB
3
；
∵2bccosA=b2+c2-a2，2abcosC=b2+a2-c2，accosB=a2+c2-b2；
∴令
b2+c2-a2
2
=
a2+b2-c2
4
=
c2+a2-b2
6
=k，
则解得，
a2=5k
c2=4k
b2=3k
；
则cosA=
b2+c2-a2
2bc
=
2k
2
12
k
=
12
12
；
故A≈73°；
同理，B≈48°；
故C=180°-73°-48°=59°．
点评：本题考查了平面向量与解三角形的应用，属于基础题．
练习册系列答案
相关题目
（
x
-
2
3x
）5的展开式中的常数项是
 
（用数字作答）．
已知函数y=loga（x+3）+6（a＞0，a≠1）的图象恒过定点M，椭圆G：
x2
a2
+
y2
b2
=1（a＞b＞0）的左，右焦点分别为F1，F2，直线l经过点M且与⊙C：x2+y2+2x-6y+9=0相切．
（1）求直线l的方程；
（2）若直线l经过点F2并与椭圆G在x轴上方的交点为P，且cos∠F1PF2=
7
25
，求△PF1F2内切圆的方程．
不等式组
(x-y+5)(x+y)≥0
0≤x≤3
，表示的平面区域是
 
．
（1）四个不同的小球放入四个不同的盒中，一共有
 
种不同的放法．
（2）四个相同的小球放入四个不同的盒中，一共有
 
种不同的放法．
（3）四个不同的小球放入四个不同的盒中且恰好有一个空盒的放法有
 
种．
某四面体的三视图如图所示，则该四面体的表面积是（　　）
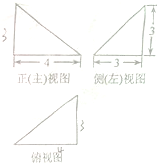
A、21B、27C、54D、60
已知n∈N*，数列{an}的首项a1=1，函数f（x）=
1
3
x3-(an+n+3)x2+2(2n+6)anx，若x=an+1是f（x）的极小值点，则数列{an}的通项公式为（　　）
A、an=
1，n=1
2n+4，n≥2
B、an=2n-1
C、an=
1    n=1
2n   n≥2
D、an=
1    n=1
2n+1  n≥2
求证：对任意的n∈N*，不等式ln
n+2
2
＜1+
1
2
+
1
3
+…+
1
n-1
都成立．
已知i为虚数单位，则复数z=
2-3i
1+i
对应的点位于（　　）
A、第一象限B、第二象限
C、第三象限D、第四象限

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网