题目内容
已知函数f(x)=2sin
cos
+
cosx.
(1)求f(x)的最小正周期;
(2)若将f(x)的图象向右平移
个单位,得到函数g(x)的图象,并求出关于x的方程g(x)=1∈,当x[0,π]时的根.
| x |
| 2 |
| x |
| 2 |
| 3 |
(1)求f(x)的最小正周期;
(2)若将f(x)的图象向右平移
| π |
| 6 |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法,函数y=Asin(ωx+φ)的图象变换
专题:计算题,三角函数的图像与性质
分析:(1)由倍角公式化简可得解析式f(x)=2sin(x+
),从而可求f(x)的最小正周期.
(2)将f(x)的图象向右平移
个单位,得到函数g(x)的解析式为g(x)=2sin(x+
),由x∈[0,π]时,可得x+
∈[
,
],从而可求方程的根.
| π |
| 3 |
(2)将f(x)的图象向右平移
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
解答:
解:(1)f(x)=2(
sinx+
cosx)=2sin(x+
)…4分
所以f(x)的最小正周期为2π.…6分
(2)∵将f(x)的图象向右平移
个单位,得到函数g(x)的图象,
∴g(x)=f(x-
)=2sin[(x-
)+
]=2sin(x+
)…9分
∵x∈[0,π]时,x+
∈[
,
],由g(x)=1得x=0或
…12分.
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
所以f(x)的最小正周期为2π.…6分
(2)∵将f(x)的图象向右平移
| π |
| 6 |
∴g(x)=f(x-
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
∵x∈[0,π]时,x+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| 2π |
| 3 |
点评:本题主要考查了三角函数中的恒等变换应用,三角函数的周期性及其求法,函数y=Asin(ωx+φ)的图象变换,属于基本知识的考查.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
某四面体的三视图如图所示,则该四面体的表面积是( )
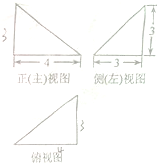

| A、21 | B、27 | C、54 | D、60 |
