题目内容
已知平面α⊥平面β，α∩β=l，点A∈α，A∉l，直线AB∥l，直线AC⊥l，直线m∥α，m∥β，则下列四种位置关系中，不一定成立的是（ ）
| A、AB∥m | B、AC⊥m |
| C、AC⊥β | D、AB∥β |
考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：由题意，画出满足条件的图形，依据面面垂直的性质以及线面平行的性质等知识解答．
解答：
解：如图所示，对于A，AB∥l∥m；A成立；
对于B，AC⊥l，m∥l⇒AC⊥m；B成立；
对于C，虽然AC⊥l，但AC不一定在平面α内，故它可以与平面β相交、平行，故不一定垂直；故不成立．
对于D，AB∥l⇒AB∥β，D成立；
故选C．
解：如图所示，对于A，AB∥l∥m；A成立；对于B，AC⊥l，m∥l⇒AC⊥m；B成立；
对于C，虽然AC⊥l，但AC不一定在平面α内，故它可以与平面β相交、平行，故不一定垂直；故不成立．
对于D，AB∥l⇒AB∥β，D成立；
故选C．
点评：本题考查了线面平行、线面垂直的判定定理及应用，本部分内容是立体几何的一个重点，要重点掌握
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
设D是函数y=f（x）定义域内的一个区间，若存在x0∈D，使f（x0）=-x0，则称x0是f（x）的一个“次不动点”，也称f（x）在区间D上存在次不动点．若函数f（x）=ax2-3x-a+
在区间[1，4]上存在次不动点，则实数a的取值范围是（ ）
| 5 |
| 2 |
| A、（-∞，0） | ||
B、（0，
| ||
C、[
| ||
D、（-∞，
|
某四面体的三视图如图所示，则该四面体的表面积是（ ）
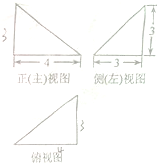
| A、21 | B、27 | C、54 | D、60 |