题目内容
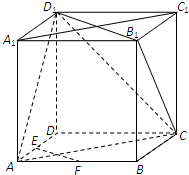如图，在正方体ABCD-A1B1C1D1中，E、F分别为棱AD、AB的中点．（1）求证：EF∥平面CB1D1；
（2）求异面直线EF与AD1所成角．
考点：异面直线及其所成的角
专题：证明题,空间位置关系与距离
分析：（1）连接BD，通过证明四边形BDD1B1为平行四边形，证明BD∥B1D1，可证EF∥B1D1，再利用线面平行的判定定理证明EF∥平面CB1D1；
（2）连接B1A，证明∠AD1B1为异面直线EF与AD1所成角，解△AD1B1可得异面直线EF与AD1所成的角．
（2）连接B1A，证明∠AD1B1为异面直线EF与AD1所成角，解△AD1B1可得异面直线EF与AD1所成的角．
解答：
解：（1）连接BD，∵E、F分别为棱AD、AB的中点．∴EF∥BD，
又DD1∥BB1且DD1=BB1，∴四边形BDD1B1为平行四边形，∴BD∥B1D1，
∴EF∥B1D1，又EF?平面CB1D1，∴EF∥平面CB1D1；
（2）连接B1A，由（1）知EF∥B1D1，∴∠AD1B1为异面直线EF与AD1所成角．
∵AD1=B1D1=AB1，
∴，∴∠AD1B1=60°，
即异面直线EF与AD1所成角为60°．
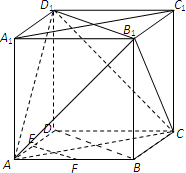
又DD1∥BB1且DD1=BB1，∴四边形BDD1B1为平行四边形，∴BD∥B1D1，
∴EF∥B1D1，又EF?平面CB1D1，∴EF∥平面CB1D1；
（2）连接B1A，由（1）知EF∥B1D1，∴∠AD1B1为异面直线EF与AD1所成角．
∵AD1=B1D1=AB1，
∴，∴∠AD1B1=60°，
即异面直线EF与AD1所成角为60°．
点评：本题考查了线面平行的证明及异面直线所成角的求法，考查了学生的空间想象能力与推理论证能力，利用作-证-求的思路求角的常用方法．
练习册系列答案
相关题目
已知等腰Rt△ABC，BC⊥AC，将△ABC绕着边AB旋转θ角到△ABC′，连接CC′，D为线段CC′的中点，P是线段AB上任一点．
已知F为抛物线E：y2=2px（P＞0）的焦点，抛物线上点G的横坐标为2，且满足|GF|=3．