题目内容
 已知等腰Rt△ABC,BC⊥AC,将△ABC绕着边AB旋转θ角到△ABC′,连接CC′,D为线段CC′的中点,P是线段AB上任一点.
已知等腰Rt△ABC,BC⊥AC,将△ABC绕着边AB旋转θ角到△ABC′,连接CC′,D为线段CC′的中点,P是线段AB上任一点.(1)求证:CC′⊥DP;
(2)当三棱锥B-ACC′的体积达到最大时,点P在线段AB的什么位置时,直线AC与平面CDP所成的角最大?为多少?
考点:棱柱、棱锥、棱台的体积,直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(Ⅰ)首先,证明AB⊥平面COC′,然后,得到CC′⊥面ABD,从而得证;
(Ⅱ)利用空间向量法:以OC,OC′OB所在直线,为x,y,z轴,建立空间直角坐标系O-xyz,写出相关的点,然后,结合向量的基本运算进行求解.
(Ⅱ)利用空间向量法:以OC,OC′OB所在直线,为x,y,z轴,建立空间直角坐标系O-xyz,写出相关的点,然后,结合向量的基本运算进行求解.
解答:
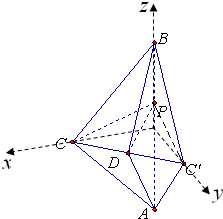 (1)证明:取AB中点O,连结OC,OC′
(1)证明:取AB中点O,连结OC,OC′
∵CB=CA,C′B=C′A,
∴CO⊥AB,C′O⊥AB,
∵OC∩OC′=O,
∴AB⊥平面COC′,
∵CC′?面COC′,
∴CC′⊥AB,
∵BC=BC′,D为CC′中点,
∴BD⊥CC′,
∵BD∩AB=B,
∴CC′⊥面ABD,
∵DP?面ABD,
∴CC′⊥DP.
(2)由 (1)得VB-ACC′=
S△OCC′•AB,
∵S△OCC′=
OC•OC′sin∠COC′,
∴当∠COC′=
时,S△OCC′取得最大值,
此时OC⊥OC′,S△OCC′达到最大,
以OC,OC′OB所在直线,为x,y,z轴,建立空间直角坐标系O-xyz,
设P(0,0,m) AB=2,则A(0,0,-1),B(0,0,1),C(1,0,0),C′(0,1,0),D(
,
,0),
=(1,0,0),
=(-
,
,0),
=(-1,0,m),
设平面CDP的法向量为
=(x,y,z),
则
,
∴
,令z=1,得x=y=m,
∴
=(m,m,1),
∴cos<
,
>=
=
令f(m)=
,m∈[-1,1],
∴f′(m)=
,
令f′(m)=0.
∴m=
,
∵m∈(-1,
),f′(m)>0.
m∈(
,1),f′(m)<0.
∴f(m)max=f(
)=
.
此时,<
,
>=
,BP=
AB,
∴当BP=
AB,直线AC与平面CDP所成的角最大,为
.
 (1)证明:取AB中点O,连结OC,OC′
(1)证明:取AB中点O,连结OC,OC′∵CB=CA,C′B=C′A,
∴CO⊥AB,C′O⊥AB,
∵OC∩OC′=O,
∴AB⊥平面COC′,
∵CC′?面COC′,
∴CC′⊥AB,
∵BC=BC′,D为CC′中点,
∴BD⊥CC′,
∵BD∩AB=B,
∴CC′⊥面ABD,
∵DP?面ABD,
∴CC′⊥DP.
(2)由 (1)得VB-ACC′=
| 1 |
| 3 |
∵S△OCC′=
| 1 |
| 2 |
∴当∠COC′=
| π |
| 2 |
此时OC⊥OC′,S△OCC′达到最大,
以OC,OC′OB所在直线,为x,y,z轴,建立空间直角坐标系O-xyz,
设P(0,0,m) AB=2,则A(0,0,-1),B(0,0,1),C(1,0,0),C′(0,1,0),D(
| 1 |
| 2 |
| 1 |
| 2 |
| AC |
| CD |
| 1 |
| 2 |
| 1 |
| 2 |
| CP |
设平面CDP的法向量为
| n |
则
|
∴
|
∴
| n |
∴cos<
| n |
| AC |
| ||||
|
|
| m+1 | ||||
|
令f(m)=
| m+1 | ||||
|
∴f′(m)=
| 1-2m | ||
(2m2+1)
|
令f′(m)=0.
∴m=
| 1 |
| 2 |
∵m∈(-1,
| 1 |
| 2 |
m∈(
| 1 |
| 2 |
∴f(m)max=f(
| 1 |
| 2 |
| ||
| 2 |
此时,<
| n |
| AC |
| π |
| 3 |
| 1 |
| 4 |
∴当BP=
| 1 |
| 4 |
| π |
| 3 |
点评:本题综合考查了空间中垂直关系、平行关系,向量及其运算等知识,属于中档题.

练习册系列答案
相关题目
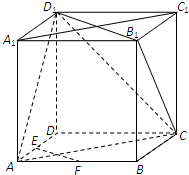 如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD、AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD、AB的中点.