题目内容
 已知F为抛物线E:y2=2px(P>0)的焦点,抛物线上点G的横坐标为2,且满足|GF|=3.
已知F为抛物线E:y2=2px(P>0)的焦点,抛物线上点G的横坐标为2,且满足|GF|=3.(Ⅰ)求抛物线E的方程;
(Ⅱ)M点的坐标为(2,0),过点F作斜率为1K的直线与抛物线交于A、B两点,A、B两点的横坐标均不为2,连结AM、BM并延长交抛物线于C、D两点,设直线CD的斜率为k2,判断
| k1 |
| k2 |
考点:直线与圆锥曲线的综合问题,抛物线的简单性质
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由抛物线定义知GF=2+
=3,由此能求出抛物线方程.
(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),则k1=
=
=
,同理k2=
,由此利用直线方程结合已知条件能求出
=2.
| p |
| 2 |
(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),则k1=
| y1-y2 |
| x1-x2 |
| y1-y2 | ||
|
| 4 |
| y1+y2 |
| 4 |
| y3+y4 |
| k1 |
| k2 |
解答:
解:(Ⅰ)由抛物线定义知GF=2+
=3,解得p=2,
∴抛物线方程为y2=4x.
(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
则k1=
=
=
,k2=
,
设AC所在的直线方程为y=m(x-2),
联立
,得my2-4y-8m=0,
∴y1y3=-8,同理,y2y4=-8,
∴
=
=
=
=
,
设直线AB的方程为y=k1(x-1),
联立
,得k1y2-4y-4k1=0,
∴y1y2=-4,
∴
=
=
=2.
| p |
| 2 |
∴抛物线方程为y2=4x.
(Ⅱ)设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
则k1=
| y1-y2 |
| x1-x2 |
| y1-y2 | ||
|
| 4 |
| y1+y2 |
| 4 |
| y3+y4 |
设AC所在的直线方程为y=m(x-2),
联立
|
∴y1y3=-8,同理,y2y4=-8,
∴
| k1 |
| k2 |
| ||
|
| y3+y4 |
| y1+y2 |
(-
| ||||
| y1+y2 |
| -8 |
| y1y2 |
设直线AB的方程为y=k1(x-1),
联立
|
∴y1y2=-4,
∴
| k1 |
| k2 |
| -8 |
| y1y2 |
| -8 |
| -4 |
点评:本题考查抛物线方程的求法,考查两直线的斜率的比值是否为定值的判断与求法,解题时要认真审题,注意直线方程的合理运用.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
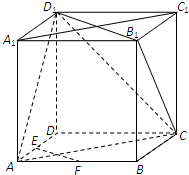 如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD、AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AD、AB的中点. 棱长为2的正方体ABCD-A1B1C1D1中,E为C1D1的中点.
棱长为2的正方体ABCD-A1B1C1D1中,E为C1D1的中点.