题目内容
已知平面向量
=（
，1），
=（
，
）．若存在不同时为零的实数k和t，使
=
+（t2-3）
，
=-k
+t
且
⊥
．
（1）试求函数关系式k=f（t）；
（2）若t∈（0，+∞）时，不等式k≥
t2+
mt恒成立，求实数m的取值范围．
| a |
| 3 |
| b |
| 1 |
| 2 |
| ||
| 2 |
| x |
| a |
| b |
| y |
| a |
| b |
| x |
| y |
（1）试求函数关系式k=f（t）；
（2）若t∈（0，+∞）时，不等式k≥
| 1 |
| 2 |
| 1 |
| 4 |
考点：函数恒成立问题,函数解析式的求解及常用方法,数量积判断两个平面向量的垂直关系
专题：函数的性质及应用
分析：（1）根据平面向量的数量积关系即可试求函数关系式k=f（t）；
（2）利用参数分离法将不等式k≥
t2+
mt恒成立进行转化，利用二次函数的图象和性质，即可求实数m的取值范围．
（2）利用参数分离法将不等式k≥
| 1 |
| 2 |
| 1 |
| 4 |
解答：
解：（1）由题知：|
|=2，|
|=1，
=0-----------------------（2分）
∵
⊥
，则
•
=[
+(t2-3)
]•(-k
+t
)=0，
整理可得：-k
2+t
•
-k(t2-3)
•
+t(t2-3)
2=-k
2+t(t2-3)
2=-4k+t(t2-3)=0，
∴k=
t(t2-3)(t≠0)．
（2）∵当t∈(0，+∞)时，不等式k≥
t2+
mt恒成立
∴
t(t2-3)≥
t2+
mt在t∈(0，+∞)上恒成立
即m≤t2-2t-3=（t-1）2-4在t∈（0，+∞）上恒成立，
∴m≤-4，
即实数m的取值范围是（-∞，-4]．
| a |
| b |
a•
|
∵
| x |
| y |
| x |
| y |
| a |
| b |
| a |
| b |
整理可得：-k
| a |
| a |
| b |
| a |
| b |
| b |
| a |
| b |
∴k=
| 1 |
| 4 |
（2）∵当t∈(0，+∞)时，不等式k≥
| 1 |
| 2 |
| 1 |
| 4 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
即m≤t2-2t-3=（t-1）2-4在t∈（0，+∞）上恒成立，
∴m≤-4，
即实数m的取值范围是（-∞，-4]．
点评：本题主要考查函数恒成立问题已经数量积的应用，利用参数分离法是解决函数恒成立问题的基本方法．
练习册系列答案
名校课堂系列答案
相关题目
已知如图，△ABC是边长为1的正三角形，PA⊥平面ABC，且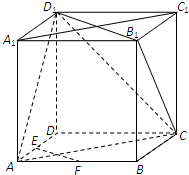
如图，在正方体ABCD-A1B1C1D1中，E、F分别为棱AD、AB的中点．
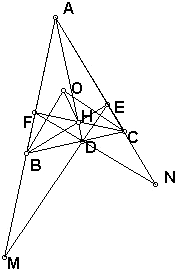如图，△ABC中，O为外心，三条高AD、BE、CF交于点H，直线ED和AB交于点M，FD和AC交于点N．求证：OB⊥DF．
棱长为2的正方体ABCD-A1B1C1D1中，E为C1D1的中点．