题目内容
若正数a，b满足
+
=1，则
+
的最小值为 ．
| 1 |
| a |
| 1 |
| b |
| 1 |
| a-1 |
| 9 |
| b-1 |
考点：基本不等式
专题：不等式的解法及应用
分析：变形利用基本不等式即可得出．
解答：
解：∵正数a，b满足
+
=1，∴b=
＞0，解得a＞1．同理b＞1
则
+
=
+
=
+9(a-1)≥2
=6，当且仅当a=
时取等号（此时b=4）．
∴
+
的最小值为6．
故答案为：6．
| 1 |
| a |
| 1 |
| b |
| a |
| a-1 |
则
| 1 |
| a-1 |
| 9 |
| b-1 |
| 1 |
| a-1 |
| 9 | ||
|
| 1 |
| a-1 |
9(a-1)•
|
| 4 |
| 3 |
∴
| 1 |
| a-1 |
| 9 |
| b-1 |
故答案为：6．
点评：本题考查了基本不等式的性质，属于基础题．
练习册系列答案
相关题目
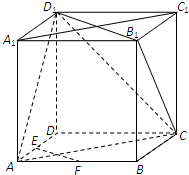如图，在正方体ABCD-A1B1C1D1中，E、F分别为棱AD、AB的中点．
棱长为2的正方体ABCD-A1B1C1D1中，E为C1D1的中点．