题目内容
两异面直线m，n分别垂直于二面角α-l-β的两个半平面，且m，n所成的角为60°，则二面角α-l-β的大小是 ．
考点：二面角的平面角及求法
专题：计算题,空间角
分析：根据二面角的定义，及线面垂直的性质，我们可得若两条直线a，b分别垂直于两个平面，则两条直线的夹角与二面角相等或互补，由于已知m，n所成的角为60°，故异面直线所成角与二面角相等或互补，即可得到答案．
解答：
解：根据二面角的定义，及线面垂直的性质，我们可得若两条直线a，b分别垂直于两个平面，则两条直线的夹角与二面角相等或互补，
∵m，n所成的角为60°，
∴二面角α-l-β的大小是60°或120°．
故答案为：60°或120°．
∵m，n所成的角为60°，
∴二面角α-l-β的大小是60°或120°．
故答案为：60°或120°．
点评：本题考查的知识点是二面角的平面角及求法，其中分别与两个平面垂直的直线的夹角与二面角相等（二面角不大于90°时）或互补（二面角大于90°时）是解答本题的关键．
练习册系列答案
相关题目
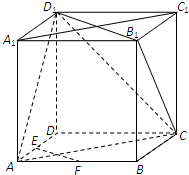如图，在正方体ABCD-A1B1C1D1中，E、F分别为棱AD、AB的中点．