题目内容
已知函数f(x)=2x+2-x.
(1)判断函数的奇偶性;
(2)求函数的单调增区间,并证明.
(1)判断函数的奇偶性;
(2)求函数的单调增区间,并证明.
考点:利用导数研究函数的单调性,函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用,导数的综合应用
分析:(1)求f(x)定义域为R,然后求f(-x)=f(x),所以得出f(x)为偶函数;
(2)求f′(x),然后找使f′(x)≥0的x所在区间,即找到了f(x)的单调增区间.
(2)求f′(x),然后找使f′(x)≥0的x所在区间,即找到了f(x)的单调增区间.
解答:
解:(1)函数f(x)的定义域为R,f(-x)=2-x+2x=f(x);
∴f(x)为偶函数;
(2)f′(x)=2xln2-2-xln2=ln2(2x-2-x);
2x≥2-x,即x≥-x,x≥0时,f′(x)≥0;
∴f(x)在[0,+∞)上单调递增,[0,+∞)是f(x)的单调递增区间.
∴f(x)为偶函数;
(2)f′(x)=2xln2-2-xln2=ln2(2x-2-x);
2x≥2-x,即x≥-x,x≥0时,f′(x)≥0;
∴f(x)在[0,+∞)上单调递增,[0,+∞)是f(x)的单调递增区间.
点评:考查奇偶函数的定义,以及根据定义判断奇偶函数的过程,函数导数符号和函数单调性的关系,指数函数的单调性.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
若直线经过A(0,0),B(0,2)两点,则直线AB的倾斜角为( )
| A、30° | B、45° |
| C、90° | D、0° |
已知f(x)=
,若f(x)=2,则x的值是( )
|
| A、-1 | ||||
B、-1或
| ||||
C、±
| ||||
D、-1或±
|
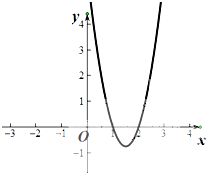 已知函数f(x)=ax3+bx2+cx+1的导函数为f′(x),y=f′(x)的图象如图所示
已知函数f(x)=ax3+bx2+cx+1的导函数为f′(x),y=f′(x)的图象如图所示