Question

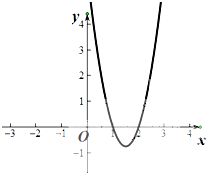已知函数f（x）=ax³+bx²+cx+1的导函数为f′（x），y=f′（x）的图象如图所示
（1）请写出f（x）单调区间；
（2）若a=1，试求函数f（x）的解析式，并求出函数f（x）的极值及取极值时的相应的x的值．

Answer 1

考点：利用导数研究函数的极值,利用导数研究函数的单调性

专题：导数的综合应用

分析：（1）由y=f′（x）的图象即可得出函数的单调区间，
（2）由图可知x=1，x=2是函数的极值点，得

f′(1)=0 f′(2)=0

，联立方程组求得b，c的值，即可得出函数的解析式，写出函数的极值．

解答： 解：（1）由图可知x＜1，或x＞2时f′（x）＞0，1＜＜2时，f′（x）＜0
∴f（x）的单调增区间是（-∞，1），（2，+∞），单调减区间是（1，2）．
（2）由图可知x=1，x=2是函数的极值点，∵a=1
∴f′（x）=3x²+2bx+c，
∴

f′(1)=0 f′(2)=0

即

3+2b+c=0 12+4b+c=0

解得b=-

9

2

，c=6．
∴f（x）=3x³-

9

2

x²+6x+1，
∴当x=1时，函数有极大值为f（1）=

11

2

，当x=2时，函数有极小值为f（2）=19．

点评：本题主要考查利用导数研究函数的单调性、单调区间、极值等知识，属于基础题，应熟练掌握．