题目内容
抛物线的顶点在原点，对称轴是x轴，抛物线上点（-5，m）到焦点距离是6，则抛物线的标准方程是（ ）
| A、y2=-2x |
| B、y2=-4x |
| C、y2=2x |
| D、y2=-4x或y2=-36x |
考点：抛物线的标准方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：设出抛物线的标准方程，再由抛物线的定义，点M到焦点的距离等于到准线的距离，即可求得抛物线方程．
解答：
解：设抛物线方程为y2=-2px（p＞0）
∵抛物线上一点（-5，m）到焦点距离是6，
∴
+5=6，
∴p=1，
∴抛物线方程为y2=-4x．
故选：B．
∵抛物线上一点（-5，m）到焦点距离是6，
∴
| p |
| 2 |
∴p=1，
∴抛物线方程为y2=-4x．
故选：B．
点评：本题考查抛物线的定义，抛物线的标准方程及其求法，利用定义将到焦点的距离转化为到准线的距离是解决本题的关键．
练习册系列答案
相关题目
已知幂函数y=f（x）的图象经过点（16，4），则f（
）的值为（ ）
| 1 |
| 64 |
| A、3 | ||
B、
| ||
C、
| ||
D、
|
集训队有6男4女共10名运动员，其中男女队长各1人，现选派5人外出参赛，则队长中至少有1人参加的选派方法共有（ ）
| A、140种 | B、126种 |
| C、196种 | D、192种 |
现有五名实习大学生分到四个班实习，每班至少分配一名，则不同分法的种数为（ ）
| A、45 | ||||
B、A
| ||||
C、C
| ||||
D、C
|
已知点P是直线2x-y+3=0上的一个动点，定点M（-1，2），Q是线段PM延长线上的一点，且|PM|=|MQ|，则Q点的轨迹方程（ ）
| A、2x+y+1=0 |
| B、2x-y-5=0 |
| C、2x-y-1=0 |
| D、2x-y+5=0 |
设z1，z2为复数，则下列四个结论中正确的是（ ）
| A、若z12+z22＞0，则z12＞-z22 | ||
B、|z1-z2|=
| ||
| C、z12+z22=0?z1=z2=0 | ||
D、z1-
|
（文）函数y=
的单调增区间是（ ）
| sinx |
A、[-
| ||||
B、[
| ||||
C、[2kπ，
| ||||
D、[
|
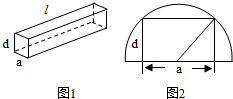如图1所示，一根水平放置的长方体枕木的安全负荷与它的宽度a成正比，与它的厚度d的平方成正比，与它的长度l的平方成反比．
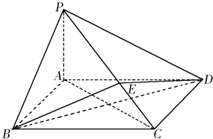如图所示，在四棱锥P-ABCD中，底面ABCD为矩形，PA⊥平面ABCD，点E在线段PC上，PC⊥平面BDE．