题目内容
已知点P是直线2x-y+3=0上的一个动点，定点M（-1，2），Q是线段PM延长线上的一点，且|PM|=|MQ|，则Q点的轨迹方程（ ）
| A、2x+y+1=0 |
| B、2x-y-5=0 |
| C、2x-y-1=0 |
| D、2x-y+5=0 |
考点：轨迹方程
专题：计算题,直线与圆
分析：确定Q，P坐标之间的关系，利用点P是直线2x-y+3=0上的一个动点，可得Q点的轨迹方程．
解答：
解：设Q（x，y），P（a，b），则
由中点坐标公式可得a=-2-x，b=4-y，
∵点P是直线2x-y+3=0上的一个动点，
∴2a-b+3=0，
∴2（-2-x）-（4-y）+3=0，即2x-y+5=0．
故选：D．
由中点坐标公式可得a=-2-x，b=4-y，
∵点P是直线2x-y+3=0上的一个动点，
∴2a-b+3=0，
∴2（-2-x）-（4-y）+3=0，即2x-y+5=0．
故选：D．
点评：本题考查轨迹方程，考查代入法的运用，比较基础．
练习册系列答案
相关题目
在数列{an}中，an-an+1=-10，a1=2，则a6=（ ）
| A、-48 | B、48 |
| C、-52 | D、52 |
当k变化时，直线kx+y-2=3k过定点（ ）
| A、（0，2） |
| B、（3，2） |
| C、（-3，2） |
| D、（3，-2） |
某校高三一班的男女同学的人数之比为3：2，用分层抽样的方法从该班的同学中抽取一个容量为5的样本，已知女同学中甲、乙两同学都被抽到的概率为
，则该班的总人数为（ ）
| 1 |
| 190 |
| A、50 | B、60 |
| C、120 | D、190 |
如图所示的程序输出的结果为（ ）
| A、17 | B、19 | C、21 | D、23 |
抛物线的顶点在原点，对称轴是x轴，抛物线上点（-5，m）到焦点距离是6，则抛物线的标准方程是（ ）
| A、y2=-2x |
| B、y2=-4x |
| C、y2=2x |
| D、y2=-4x或y2=-36x |
阅读程序（如图），若a=45，b=20，c=10，则输出的结果为（ ）
| A、10 | B、20 | C、25 | D、45 |
已知△ABC中，|
|=10，
•
=-16，D为边BC的中点，则|
|等于（ ）
| BC |
| AB |
| AC |
| AD |
| A、6 | B、5 | C、4 | D、3 |
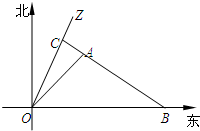如图所示，一科学考察船从港口O出发，沿北偏东α角的射线OZ方向航行，而在离港口3