题目内容
集训队有6男4女共10名运动员，其中男女队长各1人，现选派5人外出参赛，则队长中至少有1人参加的选派方法共有（ ）
| A、140种 | B、126种 |
| C、196种 | D、192种 |
考点：计数原理的应用
专题：排列组合
分析：只有男队长的选法为C84种，只有女队长的选法为C84种，男、女队长都入选的选法为C83种，把所有的结果数相加．
解答：
解：“只有男队长”的选法为C84种；
“只有女队长”的选法为C84种；
“男、女队长都入选”的选法为C83种；
∴共有2C84+C83=196种．
∴“至少1名队长”的选法有C105-C85=196种选法．
故选：C．
“只有女队长”的选法为C84种；
“男、女队长都入选”的选法为C83种；
∴共有2C84+C83=196种．
∴“至少1名队长”的选法有C105-C85=196种选法．
故选：C．
点评：本题主要考查了分类计数原理，如何分类时关键，属于基础题．
练习册系列答案
快乐小博士巩固与提高系列答案
相关题目
若实数x，y满足约束条件
，则z=2x+y的最大值为（ ）
|
| A、1 | ||
B、
| ||
| C、4 | ||
| D、6 |
将下列不同进位制下的数转化为十进制，这些数中最小的数是（ ）
| A、（20）7 |
| B、（30）5 |
| C、（23）6 |
| D、（31）4 |
n∈N*，则（20-n）（21-n）…（100-n）等于（ ）
A、A
| ||
B、A
| ||
C、A
| ||
D、A
|
当k变化时，直线kx+y-2=3k过定点（ ）
| A、（0，2） |
| B、（3，2） |
| C、（-3，2） |
| D、（3，-2） |
若点P（-1，2）在角θ的终边上，则tanθ等于（ ）
| A、-2 | ||||
B、-
| ||||
C、-
| ||||
D、
|
某校高三一班的男女同学的人数之比为3：2，用分层抽样的方法从该班的同学中抽取一个容量为5的样本，已知女同学中甲、乙两同学都被抽到的概率为
，则该班的总人数为（ ）
| 1 |
| 190 |
| A、50 | B、60 |
| C、120 | D、190 |
抛物线的顶点在原点，对称轴是x轴，抛物线上点（-5，m）到焦点距离是6，则抛物线的标准方程是（ ）
| A、y2=-2x |
| B、y2=-4x |
| C、y2=2x |
| D、y2=-4x或y2=-36x |
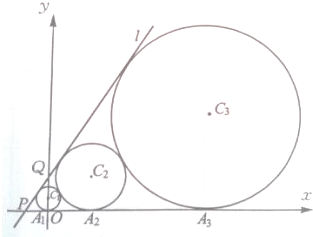如图，在平面直角坐标系中，直线l经过点P（-1，0），Q（0，