题目内容
已知A是三角形ABC的内角，则“sinA=
”是“cosA=
”的（ ）
| ||
| 2 |
| 1 |
| 2 |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：A是三角形ABC的内角，由“sinA=
”⇒A=
或
，当A=
时，推不出“cosA=
”．反之由“cosA=
”可得A=
，可得“sinA=
”．
| ||
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
解答：
解：∵A是三角形ABC的内角，由“sinA=
”⇒A=
或
，当A=
时，推不出“cosA=
”．
反之由“cosA=
”可得A=
，可得“sinA=
”．
因此“sinA=
”是“cosA=
”的必要不充分条件．
故选：A．
| ||
| 2 |
| π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
反之由“cosA=
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
因此“sinA=
| ||
| 2 |
| 1 |
| 2 |
故选：A．
点评：本题考查了充要条件的判定、三角函数的特殊值，属于基础题．
练习册系列答案
相关题目
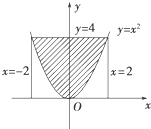如图在区域Ω={（x，y）|-2≤x≤2，0≤y≤4}中随机撒豆子，豆子落在图中阴影部分内的概率为
高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型．在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块，小木块之间留有适当的空隙作为通道，前面挡有一块玻璃．让一个小球从高尔顿板上方的通道口落下，小球在下落的过程中与层层小木块碰撞，且等可能向左向右滚下，最后掉入编号为1，2，…，7的球槽内．某高三同学试验1000次，掉入各球槽的个数统计如下：