题目内容
集合M={x|x=
,m∈Z,|m|<2,n∈N+,n≤3},用列举法表示集合M= .
| m |
| n |
考点:集合的表示法
专题:集合
分析:根据题意对n和m分别取值,逐一求出
的值,再由集合元素的互异性求出集合M.
| m |
| n |
解答:
解:由题意得,M={x|x=
,m∈Z,|m|<2,n∈N+,n≤3},
当n=1时,m可以取-1、0、1,
为-1、0、1;
当n=2时,m可以取-1、0、1,
为-
、0、
;
当n=3时,m可以取-1、0、1,
为-
、0、
;
故集合M={-1,-
,-
,0,
,
},
故答案为:{-1,-
,-
,0,
,
}.
| m |
| n |
当n=1时,m可以取-1、0、1,
| m |
| n |
当n=2时,m可以取-1、0、1,
| m |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
当n=3时,m可以取-1、0、1,
| m |
| n |
| 1 |
| 3 |
| 1 |
| 3 |
故集合M={-1,-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
故答案为:{-1,-
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题考查集合的表示方法:描述法和列举法,以及元素的互异性,注意列举时按一定的顺序做到不重不漏.

练习册系列答案
相关题目
函数f(x)=
ln
的图象可能是( )
| 1 |
| 3 |
| 1+x |
| 1-x |
A、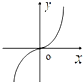 |
B、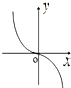 |
C、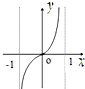 |
D、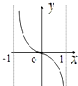 |
已知A是三角形ABC的内角,则“sinA=
”是“cosA=
”的( )
| ||
| 2 |
| 1 |
| 2 |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若U={1,2,3,4,5,6,7},A={3,4,6,7},B={3,5,6,7},则∁U(A∩B)=( )
| A、{1,2,4,5} |
| B、{2,6,8} |
| C、{1,3,5,7} |
| D、{1,2} |
