题目内容
已知向量
=(1,m+1),向量
=(m,2),且
≠
,若(
-
)⊥
.
(Ⅰ)求实数m的值;
(Ⅱ) 求向量
、
的夹角θ的大小.
| a |
| b |
| a |
| b |
| a |
| b |
| a |
(Ⅰ)求实数m的值;
(Ⅱ) 求向量
| a |
| b |
考点:数量积判断两个平面向量的垂直关系,数量积表示两个向量的夹角
专题:平面向量及应用
分析:(Ⅰ)由向量垂直时数量积为0,求出m的值;
(Ⅱ)由向量的夹角公式,结合θ的取值范围,求出
、
的夹角θ.
(Ⅱ)由向量的夹角公式,结合θ的取值范围,求出
| a |
| b |
解答:
解:(Ⅰ)∵向量
=(1,m+1),向量
=(m,2),
∴
-
=(1-m,m-1),
又∵(
-
)⊥
,
∴(
-
)•
=0,
即(1-m)+(m+1)(m-1)=0;…(4分)
∴m2-m=0,
解得m=0或m=1;…(5分)
又∵
≠
,
∴m=0;…(6分)
(Ⅱ)由(Ⅰ)得,
=(1,1),
=(0,2);
∴cosθ=
=
=
,
又∵θ∈[0,π],∴θ=
.
即向量
、
的夹角θ为
.
| a |
| b |
∴
| a |
| b |
又∵(
| a |
| b |
| a |
∴(
| a |
| b |
| a |
即(1-m)+(m+1)(m-1)=0;…(4分)
∴m2-m=0,
解得m=0或m=1;…(5分)
又∵
| a |
| b |
∴m=0;…(6分)
(Ⅱ)由(Ⅰ)得,
| a |
| b |
∴cosθ=
| ||||
|
|
| 2 | ||
|
| ||
| 2 |
又∵θ∈[0,π],∴θ=
| π |
| 4 |
即向量
| a |
| b |
| π |
| 4 |
点评:本题考查了平面向量的应用问题,考查了平面向量数量积的应用问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式(x+y-2)(x-y+1)≥0表示的平面区域时( )
A、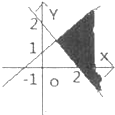 |
B、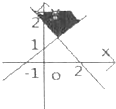 |
C、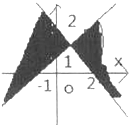 |
D、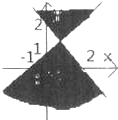 |
已知函数f(x)为偶函数,则函数f(x-1)有( )
| A、对称轴y轴 |
| B、对称中心(0,0) |
| C、对称轴x=1 |
| D、对称中心(1,0) |