已知直三棱柱ABC-A′B′C′的各顶点都在同一球面.AB=2.AC=AA′=3.BC=4.求该球的体积．题目和参考答案——青夏教育精英家教网—

题目内容

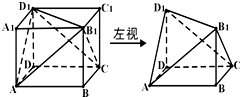
已知直三棱柱ABC-A′B′C′的各顶点都在同一球面，AB=2，AC=AA′=3，BC=4，求该球的体积．

考点：棱柱、棱锥、棱台的体积

专题：计算题,空间位置关系与距离

分析：通过已知条件求出底面外接圆的半径，确定球心为O的位置，求出球的半径，然后求出球的体积．

解答： 解：在△ABC中，AB=2，AC=3，BC=4，可得△ABC外接圆半径r=

，
设此圆圆心为O'，球心为O，在RT△OAO'中，
得球半径R=

391

，
故此球的体积为

πR³=

391

1350

5865

π．

点评：本题是中档题，解题思路是：先求底面外接圆的半径，再利用勾股定理，求出球的半径．

练习册系列答案

在△ABC中，角A，B，C的对边分别为a，b，c，且满足（2a+c）cosB+bcosC=0．
（1）求角B的值；
（2）设

为了研究玉米品种对产量的影响，某农科院对一块试验田种植的一批玉米共10000株的生长情况进行研究，现采用分层抽样方法抽取50株为样本，统计结果如表：

	高茎	矮茎	合计
圆粒	11	19	30
皱粒	13	7	20
合计	24	26	50

（1）现采用分层抽样方法，从这个样本中取出10株玉米，再从这10株玉米中随机选出3株，求选到的3株之中既有圆粒玉米又有皱粒玉米的概率；
（2）根据对玉米生长情况作出的统计，是否能在犯错误的概率不超过0.050的前提下认为玉米的圆粒与玉米的高茎有关？（下面的临界值表和公式可供参考）：

P（K²≥k）	0.15	0.10	0.050	0.025	0.010	0.001
k	2.072	2.706	3.841	5.024	6.635	10.828

K²=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

，其中n=a+b+c+d为样本容量．

哈三中高二某班为了对即将上市的班刊进行合理定价，将对班刊按事先拟定的价格进行试销，得到如下数据：

单价x（元）	8	8.2	8.4	8.6	8.8	9
销量y（元）	90	84	83	80	75	68

）
（Ⅱ）预计今后的销售中，销量与单价服从（Ⅰ）中的关系，且班刊的成本是4元/件，为了获得最大利润，班刊的单价定为多少元？

设函数f（x）=

|x+1|+|x-2|+a

．
（1）当a=-5时，求函数f（x）的定义域；
（2）若存在正数a使函数f（x）的最小值为2且正数m，n满足m+2n=a，试求m²+n²最小值．

如图，在正方体ABCD-A₁B₁C₁D₁中，异面直线A₁B与AC所成的角是

°．

在平面直角坐标系xOy中，直线l的参数方程为

x=3-

（t为参数）．在极坐标系（与直角坐标系xOy取相同的单位长度，且以原点O为极点，以x轴正半轴为极轴）中，圆C的方程为ρ=2

sinθ．
（Ⅰ）求圆C的直角坐标方程；
（Ⅱ）设圆C与直线l交于A，B两点，若点P坐标为（3，

），求|PA|•|PB|的值．

已知函数f（x）=2cosx（cosx+

sinx）+a（x∈R，a∈R，a是常数）．
（Ⅰ）求函数y=f（x）的单调递增区间；
（Ⅱ）若x∈[0，

]时，函数f（x）的最大值为4，求a的值．

试题分类